数学基础
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2082页(1577字)
旋转矩阵: 设0-xyz为固定坐标系。在杆件上取一点0'作连体参考坐标系0'-ξηζ。固定坐标轴上的单位矢量为i,j,k,参考坐标轴上的单位矢量为f,g,h。于是,旋转矩阵为:
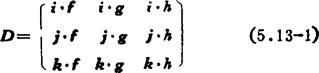
齐次变换矩阵: 设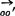 =P(这里0'不是杆件的质心)。杆件上任意一点P在固定坐标中的位置为Pxyz=〔PxPyPz〕,同一点在参考坐标中的位置为Pξηζ=〔PξPηPζ〕,如图5.13-30所示,则
=P(这里0'不是杆件的质心)。杆件上任意一点P在固定坐标中的位置为Pxyz=〔PxPyPz〕,同一点在参考坐标中的位置为Pξηζ=〔PξPηPζ〕,如图5.13-30所示,则
Pxyz=p+DPξηζ (5.13-2)
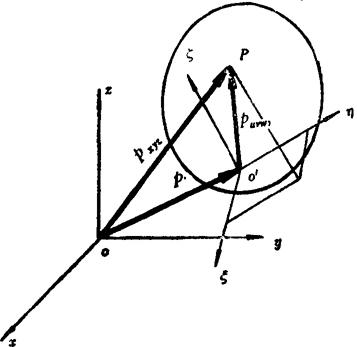
图5.13-30 杆件上一点P的坐标
右边第一项表示移动变换,第二项表示转动变换。为了把移动变换和转动变换用矩阵表示,定义4×1矢量
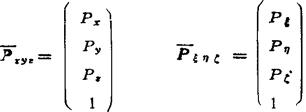
(5.13-3)
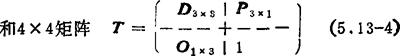
于是(5.13-2)式成为

称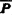 xyz为矢量Pxyz的齐次坐标。4×4矩阵T同时表示参考坐标系的位置和方位,称为齐次变换矩阵。齐次变换矩阵可用来表示一个参考坐标系在固定坐标系中的位置和方位;同时表示空间一点在原点不重合时的参考坐标和固定坐标之间的坐标变换关系;又可表示参考坐标系相对于固定坐标系的移动和转动。下面求T的逆:
xyz为矢量Pxyz的齐次坐标。4×4矩阵T同时表示参考坐标系的位置和方位,称为齐次变换矩阵。齐次变换矩阵可用来表示一个参考坐标系在固定坐标系中的位置和方位;同时表示空间一点在原点不重合时的参考坐标和固定坐标之间的坐标变换关系;又可表示参考坐标系相对于固定坐标系的移动和转动。下面求T的逆:
由(5.13-5)式得:Pξηζ=T-1Pxyz (a)
由(5.13-2)式得:Pξηζ=-DTp+DTPxyz (b)

这里T-1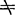 TT。设操作手末端夹持器的参考坐标轴上单位矢量的固定坐标的投影列阵为n、8和a,则
TT。设操作手末端夹持器的参考坐标轴上单位矢量的固定坐标的投影列阵为n、8和a,则
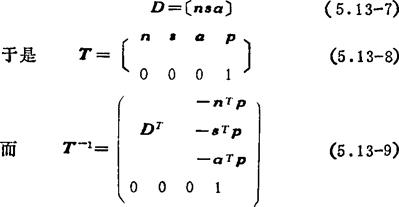
基本齐次变换矩阵:绕x轴转动a角的基本齐次转动矩阵为
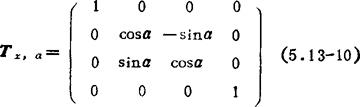
类似,绕y轴转动Φ角和绕z轴转动θ角的转动矩阵为:
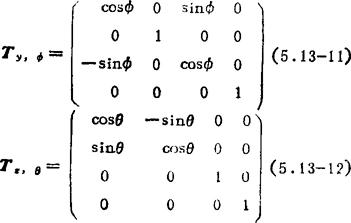
设沿x,y和:轴方向的移动分别为dx、dy和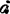 z,则基本齐次移动矩阵为
z,则基本齐次移动矩阵为
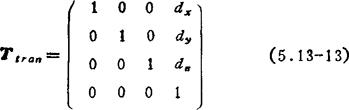
齐次变换矩阵的合成:矩阵合成时必须注意矩阵乘法的次序。设开始时参考坐标系0'-ξηζ和固定坐标系0-xyz是重合的,因此齐次变换矩阵T是4×4的单位矩阵I4。由(5.13-5)式可知,空间一点P的位置坐标在参考坐标系和固定坐标系是相同的。如果参考坐标系连同点P一起绕固定坐标系轴x,y和z移动或转动,则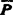 ξηζ已知,而
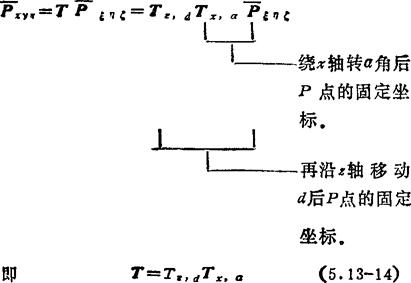
ξηζ已知,而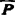 xyz是未知的。例如参考坐标和点P先绕x轴转a角,再沿z轴移动d,则合成的齐次变换矩阵为
xyz是未知的。例如参考坐标和点P先绕x轴转a角,再沿z轴移动d,则合成的齐次变换矩阵为
如果固定坐标系连同P点一起绕参考坐标系轴ξ,η和ζ移动或转动,则 已知,而
已知,而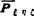 是未知的。例如固定坐标和点P绕ξ轴转a角,沿ζ轴移动d.则P点在参考坐标系中的位置依次变换为
是未知的。例如固定坐标和点P绕ξ轴转a角,沿ζ轴移动d.则P点在参考坐标系中的位置依次变换为
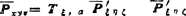 ——绕ξ轴转a角后P点的参考坐标。
——绕ξ轴转a角后P点的参考坐标。
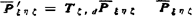 ——再沿ζ轴移动d后P点的参考坐标。
——再沿ζ轴移动d后P点的参考坐标。
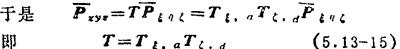
相应的基本齐次变换矩阵右乘原来的齐次变换矩阵。
基本齐次变换矩阵Tx,a和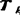 .a、
.a、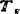 ,d和Tζ,完全相同,但因乘法次序不同其意义也跟着不同。
,d和Tζ,完全相同,但因乘法次序不同其意义也跟着不同。