连杆曲线及其方程

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2105页（2216字）

连杆曲线，是连杆机构中连杆平面上的点，在机架坐标平面内的轨迹曲线。随着发生点在连杆平面上的不同位置，连杆曲线具有各种不同的形状，如图5．15-1所示。具有全周转动构件的四杆机构(即满足曲柄存在条件的四杆机构)，因为可以有两种装配型式，即存在两个运动域。所以，其连杆上某一点有两条不能过渡的轨迹曲线，如图5．15-2所示。不满足曲柄存在条件的全摇杆机构，因为只有一种装配型式，因而其连杆上某一点只有一条轨迹曲线，如图5．15-3所示。对于最短杆与最长杆长度之和等于另两杆长度之和的四杆机构，则具有运动不确定位置。在这一位置，机构可以由一种装配型式过渡到另一种装配型式。如图5．15-4所示的平行四边形机构，其C点的连杆曲线为圆。但该机构也能进入另一运动域而以反平行四边形机构运动。这时，C点(图上标为C＇)的连杆曲线是一条四阶二重虚圆点曲线。这条曲线与圆一起构成的全部连杆曲线，是具有五个二重点的六阶曲线。

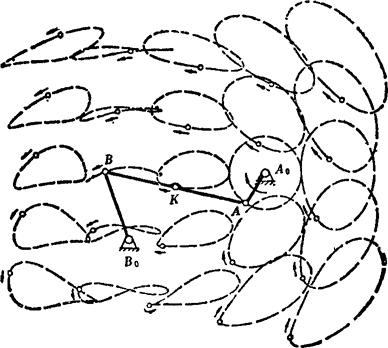
图5．15-1 连杆曲线

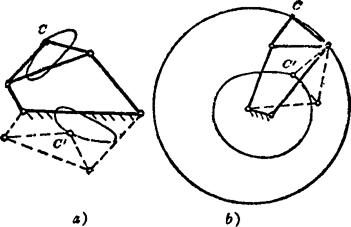
图5．15-2 连杆曲线(含2条)

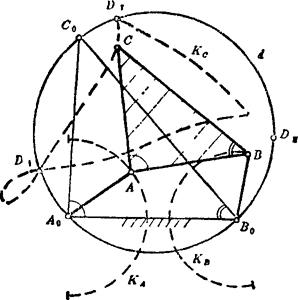
图5．15-3 连杆曲线(单条)

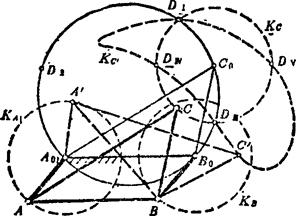
图5．15-4 平行四边形机构的连杆曲线

含有移动副的四杆机构产生的连杆曲线与铰链四杆机构产生的连杆曲线，具有不同的阶数和重数。摇杆滑块机构的连杆曲线是一条四阶虚圆点代数曲线，其两个有限远二重点D_Ⅰ和D_Ⅱ与铰链中心A₀位于一条直线d上，如图5．15-5所示。双滑块机构的连杆曲线是椭圆。滑块导杆机构的连杆曲线是蚌线，如图5．15-6所示。只有曲柄导杆机构和摇杆导杆机构的连杆曲线，显示出与铰链四杆机构的连杆曲线有相同的性质。

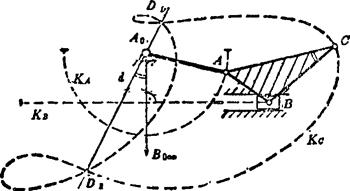
图5．15-5 摇杆滑块机构的连杆曲线

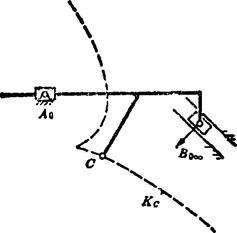
图5．15-6 滑块导杆机构的连杆曲线

为研究连杆曲线，需要导出连杆曲线的直角坐标方程式。对于铰链四杆机构，连杆平面ABC上的C点在运动时，其行经的轨迹就是连杆曲线，因此，可按C点的坐标来讨论连杆曲线。其坐标取法及各杆长和角度的代表符号如图5．15-7所示，可得如下形式的连杆曲线方程式：

U²+V²=W² 5．15-1

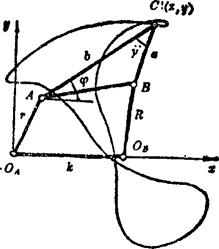
图5．15-7 铰链四杆机构坐标取法及符号

式中 U=a〔(x－k)cosγ+ysinγ〕(x²+y²+b²－，²)－bx〔(x－k)²+y²+a²－R²〕

V=a〔(x－k)sinγ-ycosγ〕(x²+y²+b²－r²)+by〔(x－k)²+y²+a²－R²〕

W=2absinγ〔x(x－k)+y²－kyctgγ〕

在以上各式中，U、V是三次方程，W是二次方程，故铰链四杆机构的连杆曲线应为六阶曲线。

图5．15-8所示为曲柄滑块机构，坐标取法及各杆长和角度的代表符号如图示，其连杆平面ABC上的C点的轨迹曲线方程为：

U2+V²=W² 5．15-2

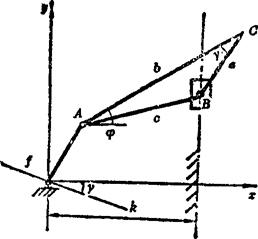
图5．15-8 曲柄滑块机构坐标取法及符号

式中 U=2bx(x－k)+acosγ〔r²－(x²+y²+b²)〕

V=asinγ〔r²－(x²+y²+b²)〕－2by(x－k)

W=－2ab(xsinγ+ycosγ)

式(5．15-2)形式上与式(5．15-1)相同，但在这里，U、V均为二次方程而不是三次方程，故曲柄滑块机构的连杆曲线为四阶曲线。但对曲柄滑块机构来说，满足曲柄存在条件的机构可以有两种装配形式，因此，其连杆曲线有两条，如图5．15-9所示，

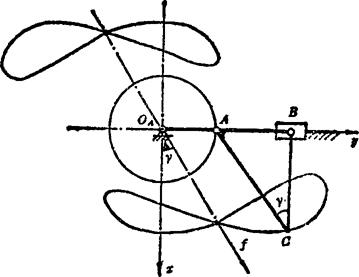
图5．15-9 连杆曲线(含2条)

导杆机构，其坐标取法及各杆长和角度的代表符号如图5．15-10所示，连杆曲线的方程为：

U²+V²=W² 5．15-3

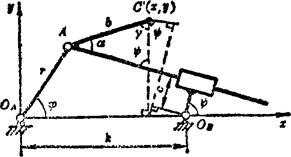
图5．15-10 导杆机构坐标取法及符号

式中 U=(k－x)(x²+y²+b²－r³)+2b(6+bsina)(xsina-ycosa)

V=y(x²+y²+b²－r²)－2b(e+bsina)(xcosa+ysina)

W=2bcosa〔x(x－k)+y²－kytga〕

因此，导杆机构的连杆曲线为六阶曲线。