矩阵与行列式

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第16页（4699字）

6．1．1 矩阵及其秩

数域F上的m×n个数aij(i=1，2，…，m；j=1，2，…，n)按确定的位置排成的矩形阵列，称为m×n矩阵，记作

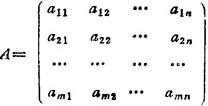
由矩阵任一行的元素构成n维矢量，称为行矢量，记为αi=(a_i1，a₁₂，…，a_1n)(i=1，2，…，m)；由矩阵任一列的元素构成m维矢量，称为列矢量，记为

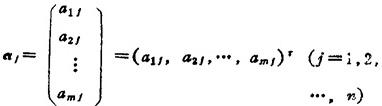
若矩阵A的n个列矢量中r个线性无关(r≤n)，而所有个数大于r的列矢量组都线性相关，则称数r为矩阵A的列秩。类似可定义矩阵A的行秩。

①此曲面也是直纹面。

矩阵A的列秩与行秩一定相等，统称矩阵的秩，记为rankA=r。

6．1．2 行列式

是由排成n阶方阵形式的n²个数a₁(i，j=1，2，…，n)确定的一个数其值为n1项之和

D=Σ(－1)^ka_1k1a_2k2…ankn

式中k₁，k₂，…k_n是将序列1，2，…，n的元素次序交换k次所得到的一个序列；Σ表示对k₁，k₂…，k_n取遍1，2，…n的一切排列求和。

从n阶行列式D中任取k行和k列(1≤k≤n－1)，由这k行与k列交点处的元素构成的k阶行列式称为行列式D的k阶子式。

如果所选取的k行k列分别是第i₁，i₂，…i_k行与第i₁，i₂，…，i_k列，则所得的k阶子式称为主子式。

从行列式D中划去k行与k列后得到的n－k阶行列式称为子式M的余子式M^′。通常用Mif表示划去a₁₁所在行和列后余下的n－1阶子式，用A_if=(－1)¹⁺¹M_if表示a_1f的代数余子式。且有

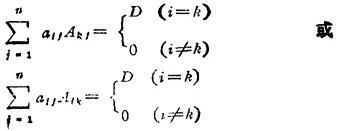
6．1．3 行列式的性质

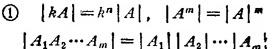
|A₁A₂…A_m|=|A₁||A₂|…|_Am|

式中 A₁，A₂，··A_m全为n阶方阵。

②行与列互换后行列式的值不变，即

|A′|=|A|

③互换行列式的任意两行(或列)，行列式变号。

④用数k乘行列式的一行(或列)，等于将行列式乘以数k。

⑤将行列式的一行(或列)乘以数k后加到另一行(或列)的相应元素上，行列式的值下变。

⑥若行列式中有一行(或列)全为零，则行列式等于零。

⑦若行列式中某一行(或列)的所有元素都可表示为两项之和，则该行列式可用两个同阶的行列式之和来表达。例如：

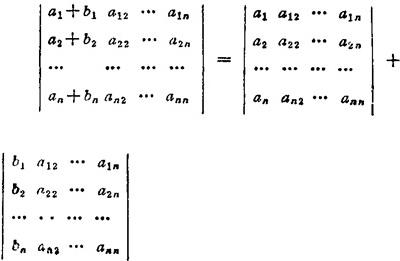
6．1．4 矩阵的初等变换

矩阵的初等变换是指：

①交换矩阵的两行(列)；

②用一个不为零的数乘某一行(列)；

③用一个数乘某一行(列)后加到另一行(列)的相应元素上。

初等变换不改变矩阵的秩。

6．1．5 特殊矩阵

(1)对角矩阵

除主对角线以外的元素都是零(a_if=0，i≠j)的方阵，记作：

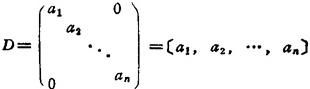
当a_i=1(i=1，2，…n)的数量矩阵称为单位矩阵。

(2)对称矩阵

满足条件a_if=α_fi(i，j=1，2，…n)的方阵A=(a_if)称为对称矩阵。对称矩阵具有性质：若A、B都是对称矩阵，则A^′=A，且A^－1，A^m(m为正整数)，A+B仍是对称矩阵。

(3)实对称矩阵

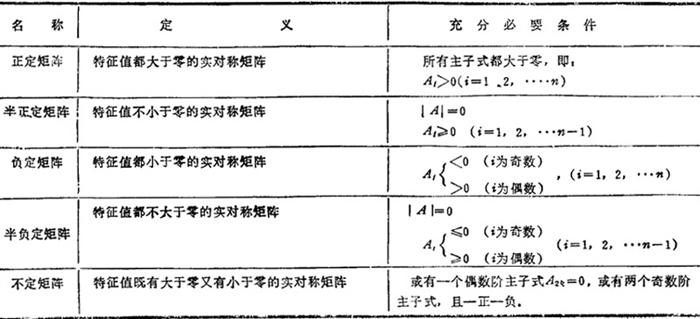
实对称矩阵按其特征值可分为正定矩阵、半正定矩阵、负定矩阵、半负定矩阵和不定矩阵，它们的定义和充要条件如表1．1－9所列。

表1．1－9 实对称矩阵

(4)反对称矩阵

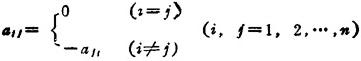
满足条件的方阵A=(a_if)称反对称矩阵。反对称矩阵具有如下性质：

①若A，B都是反对称矩阵，则A^－1，A′=－A，A+B仍是反对称矩阵，

Am为｛对称矩阵 (m为偶数)

反对称矩阵 (m为奇数)

②任意方阵A都可分解为一个对称矩阵B=(b₁₁)与一个反对称矩阵C=(C_if)之和，即

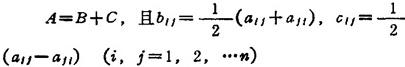
(5)正交矩阵

满足条件A′=A^－1的方阵称为正交矩阵。正交矩阵具有如下性质：

若A=(a₁₁)和B都是正交矩阵，则

①A^－1，AB仍是正交矩阵。

②|A|=±1。

③

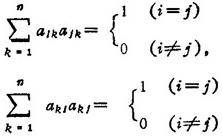
(6)三角矩阵

满足条件a_i1=0(i＞j)的方阵A=(a_if)称为上三角矩阵，一般形式为：

满足条件b1_if=0(i＜j)的方阵B=(b_if)称为下三角矩阵，一般形式为：

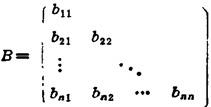
三角矩阵具有如下性质：

①任何方阵C都可表示成一个上三角矩阵A

和一个下三角矩阵B的乘积，即C=AB。

②上(下)三角矩阵的和、差、积和数乘仍是上(下)三角矩阵。

6．1．6 矩阵的相似变换

(1)相似变换

如果有一非奇异矩阵X使得B=X－1AX，那么称矩阵A与矩阵B相似，也称A经相似变换化为B，记作A～B。它具下列性质：

① A～A，A′～A；

② 若A～B，则B～A；

③ 若A～C，B～C，则A～B2

④ X^－1AmX=(X^－1AX)^m；

⑤ X^－1(A₁+A₂+…+A_m)X=X^－1A₁X+X^－1A₂X+…+X^－1A_mX；

⑥ X^－1(A₁A₂…A_m)X=X^－1A1X·X^－1A₂X…X^－1A_mX：

⑦ 若f(A)为矩阵A的多项式，则X^－1f(A)X=f(X^－1AX)；

⑧ 若A～B，则A与B的秩，A与B的行列式，A与B的迹，A与B的特征多项式和特征值均相同。

(2)正交变换

若Q为正交矩阵(即Q－1=Q′)，则称Q′AQ为矩阵A的正交变换。其性质与相似变换类似，且对称矩阵A经正交变换后仍是对称矩阵。

6．1．7 逆矩阵

若方矩A、B满足等式AB=BA=I(I为单位矩阵)，则称A为B的逆矩阵，或称B为A的逆矩阵，记作：A=B－1或B=A^－1。此时A、B都称为可逆矩阵。可逆矩阵具有如下性质：

①若A，B为可逆矩阵，则AB仍为可逆矩阵，且(AB)^－1=B^－1A^－1。一般地，若A₁，A₂，…Am均为可逆矩阵，则

(A₁A₂…A_m)^－1=Am^－1…A₂^－1A₁^－1

②矩阵A可逆的充要条件为|A|≠0，或矩阵A的特征值全不为零。

③若矩阵A可逆，则

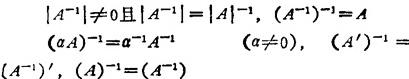
6．1．8 矩阵的特征值与特征矢量

(1)特征值与特征矢量

对于n阶方阵A和n维非零列矢量a=(a₁，a₂，…a_n)^r，如果有一个数λ使得Aa=λα，则称λ为矩阵A的特征值，a为矩阵A的特征值λ所对应的特征矢量。称A所有特征值中绝对值最大的一个为A的第一特征值。

(2)特征矩阵、特征多项式，特征方程

n阶方阵A的特征矩阵定义为：

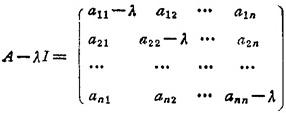
式中I为n阶单位矩阵。行列式|A－λI|称为矩阵A的特征多项式，记作φ(λ)=|A－λI|，方程φ(λ)=0称为矩阵A的特征方程。