传递函数
书籍:现代综合机械设计手册上
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第384页(837字)
传递函数是经典控制理论中最常用的一种数学模型,只适用于线性定常连续系统,线性定常连续系统的传递函数定义为:在零初始条件下,系统输出量拉氏变换与输入量拉氏变换之比。通常用符号G(s)表示,若设线性定常连续系统微分方程一般形式为

式中 c(t)为系统输出量;r(t)为系统输入量。对式(1.9-19)两端取拉氏变换,当初始条件为零时,即
c(0)=c((1)(0)=c(1)(0)=…=c(n-1)(0)=0
r(0)=r(1)(0)=r(2)(0)=…=r(m-1)(0)=0
则有 (ansn+an-1sn-1+…+a1s+a0)c(s)=(bmsm+bm-1sm-11+…+b1s+b0)R(s)
于是可得线性定常系统的传递函数一般形式

例1.9-4 图1.9-15(a)所示为组合机床动力滑台系统,该系统在理想工作状态下,滑台应平稳工作。但在有随时间变化的切削力f(t)的作用下,滑台会产生往复振动,振动位移为x(t),从而降低被加工工件的表面质量。为分析这一动态过程,可将该系统简化为图1.9-15(b)所示质量—阻尼—弹簧系统,试推导该系统的传递函数。

图1.9-15 动力滑台系统
解:该系统输入量为f(t),输出量为x(t),应用牛顿第二定律,可列出该系统的运动方程为

在零初始条件下对上式两端取拉氏变换后,可得传递函数
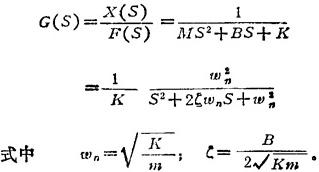
上一篇:方框图与闭环系统的传递函数
下一篇:稳定裕量