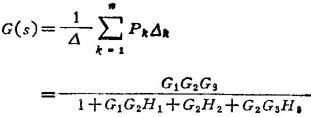方框图与闭环系统的传递函数

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第390页（1777字）

2．6．1 方框图的组成及其简化方法

方框图是描述系统运动特性的数学图形，由带箭头的信号线、方框、加减点(综合点)、引出点(分支点)等元素组成，如表1．9－3所示。

表1．9－3 组成方框图的元素

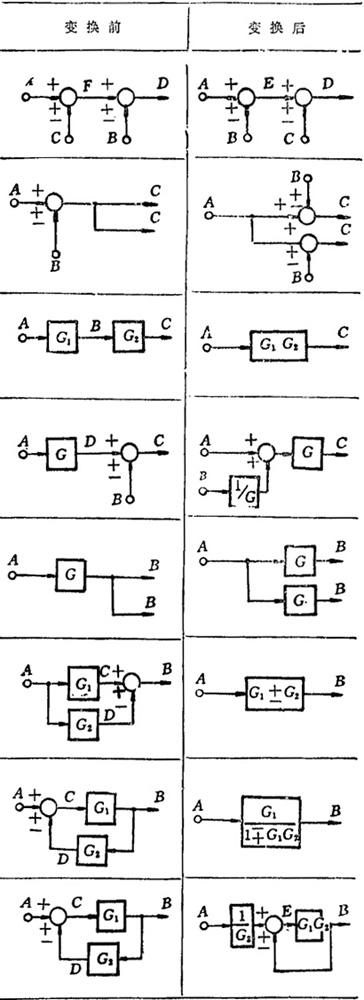
根据系统或元件的各运动方程式绘制而成的方框图，往往是很复杂的。为了便于分析系统，便于由方框图求出系统的传递函数，通常要对方框图进行简化。简化方框图所使用的等效变换基本法则如表1．9－4所示。

表1．9－4 方框图等效变换法则

例1．9－6 利用方框图等效变换求图1．9－20所示系统传递函数C(s)／R(s)。

图1．9－20 例1．9－6系统方框图

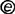方框图简化过程如图1．9－21所示。即：引出点@、⑤后移；消除反馈；消除反馈：消除反馈．得

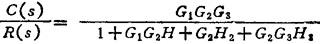
图1．9－21 方框图简化

2．6．2 闭环系统的传递函数

任何复杂的方框图，经简化后，都可变成图1．9－22所示一般形式。由该图给出系统开环传递函数、闭环传递函数等的定义。

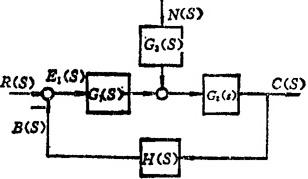
图1．9－22 方框图的一般形式

R(s)－输入量，C(s)－输出量，B(s)－反馈信号，N(s)－扰动量，E₁(s)－偏差

反馈信号B(s)与偏差信号E₁(s)之比称为开环传递函数，即

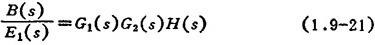
系统工作时，由于输入信号和扰动同时存在，所以对闭环传递函数可利用叠加原理分别定义系统在输入信号作用下的闭环传递函数和在扰动作用下的闭环传递函数。

令扰动量N(s)=0，闭环系统的输出量C(s)与输入量R(s)之比称为系统在输入信号作用下的传递函数，简称闭环传递函数，一般以Φ(s)表示，

当反馈通道传递函数H(s)=1时，系统称单位反馈系统，其闭环传递函数可写成

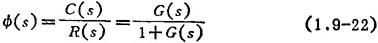
式中 G(s)==G₁(s)G₂(s)。

令输入量R(s)=0，闭环系统的输出量C(s)与扰动量N(s)之比称为系统在扰动作用下的闭环传递函数，一般以ΦN(s)表示，即

2．6．3 梅逊公式

对任意结构的方框图，其两变量之间的传递函数可用下面的梅逊公式求出：

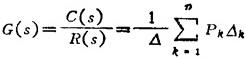
式中 n为前向通路的条数：P_k为第k条前向通路的传递函数；△=1－∑L_a+∑L_bL_c－∑L_dL_aL_f+…，为方框图的特征式；∑L_a是所有反馈回路的开环传递函数之和；∑L_bL_c是每两个互不接触的反馈回路的开环传递函数乘积之和；∑L_dL_aL_f是每三个互不接触的反馈回路的开环传递函数乘积之和；…；△k为第k条前向通路的余因子式，即在方框图中，把与第k条前向通路相接触的反馈回路除去以后的△值。

例1．9－7 利用梅逊公式计算例1．9－6方框图所示系统的传递函数C(s)／R(s)。

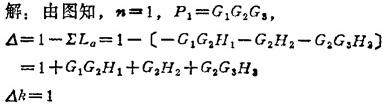
于是可得该系统传递函数为