三角函数的性质
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第39页(2393字)

例1 下列函数中,既为偶函数又在(0,π)上单调递增的是( ).
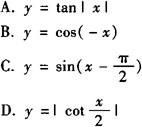
解 观察四个选项知四个函数都是偶函数,故只须判断哪个函数在(0,π)上单调递增即可,结合三角函数的图象知答案为C.
例2 已知函数f(x)=cos4x—2sinxcosx—sin4x.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若x∈[0,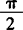 ],求f(x)的最大值、最小值.
],求f(x)的最大值、最小值.
分析 本题主要考查三角函数的倍角、和角公式,以及三角函数的性质等基本知识,考查运算能力.
解 (Ⅰ)
因为f(x)=cos4x—2sinxcosx—sin4x.
=(cos2x+sin2x)(cos2x—sin2x)—sin2x
=cos2x—sin2x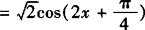 ,
,
所以f(x)的最小正周期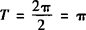 ,
,
(Ⅱ)因为 ,所以
,所以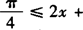
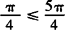 .
.
当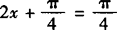 时,
时,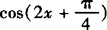 取得最大值
取得最大值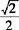 ;当
;当 时,
时,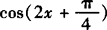 取得最小值—1,所以f(x)在[0,
取得最小值—1,所以f(x)在[0,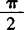 ]上的最大值为1,最小值为
]上的最大值为1,最小值为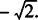 .
.
例3 求下列函数的定义域.
①f(x)=logsinx(1+2cosx);
②f(x)=lg(sinx—cosx).
分析 解这类题实际上就是解三角不等式或不等式组,要充分利用单位圆和三角函数的图象辅助求解,对三角不等式组要将各个不等式的解的区域在单位圆中表示出来后,求得公共区域,再写出其解集.
解①
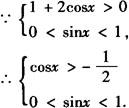
画出单位圆,标出各不等式的解的区域则公共区域一目了然,即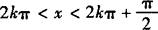 或
或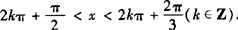 .
.
故f(x)的定义域为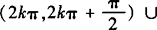
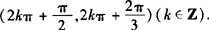
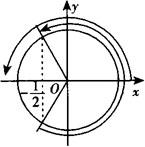
②由题意知sinx—cosx>0,即sinx>cosx
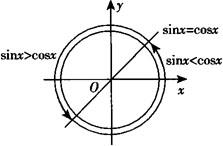
由单位圆中的三角函数线图知,直线y=x的左上方区域即是sinx>cosx的解的区域.
∴f(x)的定义域为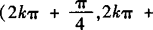
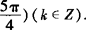 .
.
例4 求下列函数的值域:
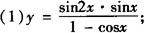
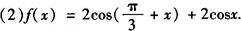
分析 将原函数式化为y=Asin(ωx+φ)+B,y=Acos(ωx+φ)+B型,或化为关于sinx(或cosx)的二次函数式,利用换元法进行配方可解决问题.
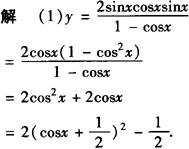
∴ymax=4,当且仅当cosx=1时取得,但cosx≠1,∴y<4.
∴ymin=—1/2,当且仅当cosx=—1/2时取得.故该函数的值域为[—1/2,4).
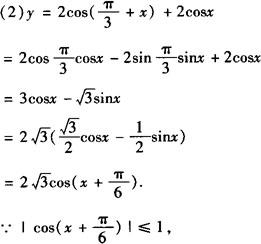
∴该函数的值域为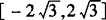 .
.
评析 在求函数的值域时,应注意其定义域.
例5 判断下列函数的奇偶性:
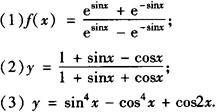
解 (1)定义域为esinx—e—sinx≠0,
∴sinx≠0 即x≠kπ(k∈Z)定义域关于原点对称.
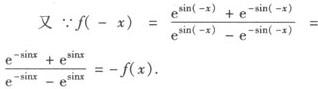
∴该函数是奇函数.
(2)∵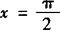 时,1+sinx+cosx=2,而
时,1+sinx+cosx=2,而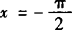 时,1+sinx+cosx=0函数无意义,
时,1+sinx+cosx=0函数无意义,
∴函数的定义域不关于原点对称.∴该函数既不是奇函数也不是偶函数.
(3)∵y=sin4x—cos4x+cos2x
=(sin2x+cos2x)(sin2x—cos2x)+cos2x
=—cos2x+cos2x=0,
∴该函数既是奇函数,又是偶函数.
评析 讨论函数奇偶性应先考虑函数定义域是否关于原点对称,是函数为奇、偶函数的必要条件.