直线方程的几种形式
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第62页(1871字)
1.点斜式 若直线l的斜率是k,并且经过点P1(x1,y1),则它的方程是y—y1=k(x—x1).
【说明】当直线l的倾斜角为0°时,它的方程是y=y1,当直线l的倾斜角为90°时,直线l没有斜率,这时直线l与y轴平行或重合,它的方程是x=x1.
2.斜截式 若直线l的斜率是k,与y轴的交点是(0,b)(b称为直线l在y轴上的截距),则它的方程是y=kx+b.
3.两点式 若直线l经过两点P1(x1,y1),P2(x2,y2)(x1≠x2,y1≠y2),则它的方程是 .
.
4.截距式 若直线l在x轴和y轴上的截距分别是a和b(a≠0,b≠0),则它的方程是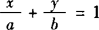 .
.
5.一般式 因为直线的方程都可以写成关于x、y的一次方程,关于x和y的一次方程都表示一条直线,所以,我们把方程Ax+By+C=0(其中A、B不全为零)叫做直线方程的一般式.
例1 已知直线l经过P(2,1)且它的倾斜角为已知直线l′∶3x—4y—17=0的倾斜角的1/2,求l的方程.
解 设直线l′的倾斜角为α,则直线l的倾斜角为 .
.

故所求直线方程为:
x—3y+1=0.
例2 经过点A(1,2),并且在两个坐标轴上的截距的绝对值相等的直线方程有( ).
A.1条 B.2条
C.3条 D.4条
解 设直线在x轴,y轴上的截距分别为a,b,则|a|=|b|,即a=±b.
若a=b=0,则直线方程为y=kx.
∵直线过A(1,2),∴k=2,∴直线方程为y=2x.

若a=b,则a=b=3,
∴直线方程为x+y—3=0;
若a=—b,则a=—1,b=1,
∴直线方程为x—y+1=0.
∴满足条件的直线有3条,故选C.
点评 本题引起分类讨论的因素有两个方面:一是直线是否过原点;二是|a|=|b|,则a=±b.容易漏解的原因是忽视直线过原点的情况.
例3 求经过两点A(2,1)和B(m,2)(m∈R)的直线l的斜率,并求出其倾斜角α及其取值范围.
解 ∵当m=2时,x1=x2=2,
∴直线l垂直于x轴,故其斜率不存在,此时,倾斜角 .
.

例4 当a为任意实数时,直线(a—1)x—y+2a+1=0恒过定点,试确定这个定点.
解 设直线恒过定点(x0,y0),则(a1)x0—y0+2a+1=0.
∵a(x0+2)+(—x0—y0+1)=0对一切a∈R都成立,
∴x0+2=0,—x0—y0+1=0,
∴x0=—2,y0=3,即定点为(—2,3).
点评 所谓恒过定点,即与方程中a的取值无关,恒过定点的问题是直线方程中的重点题型.