句法悖论

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第59页（618字）

只涉及句法概念和数学概念的悖论，是逻辑或数学形式系统中的矛盾。

主要的句法悖论有：(1)1897年，布拉里－弗蒂(Bwrali－Forti)表述的最大序数的悖论；(2)1899年，康托(G·Cantor)表述的最大基数的悖论；(3)1902年，罗素(B．Russell)提出的“所有不以自身为元素的集合的集合”的悖论；(4)“相互之间没有关系的两个关系之间的关系”的悖论，等等。其中，罗素悖论影响最大。

弗雷格说，这个悖论动摇了他企图建立算术的逻辑体系的基础。

康托悖论可表述如下：根据集合论中的康托定理，任一集合m的幂集的基数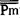大于m的基数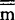，即。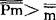

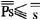设S为所有集合的集合。一方面，由康托定理有；另一方面，PS又是S的子集，有，矛盾。

罗素悖论可表述如下：设S为“所有不以自身为元素的集合的集合”，即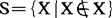。那么，S是否属于S呢?如果S∈S，由S的定义，S不是自身的元素，即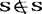；如果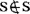，由S的定义，S属于S，即S∈S。于是，S∈S，当且仅当。

形式系统中句法悖论的主要原因是构造集合的概括公理的极端任意性和形式化方法的高度抽象性，割裂了内在于集合中的完成性与过程性的辩证矛盾，并使双方机械地对立。关于句法悖论的主要理论有：类型论、公理集合论、直觉交叉的观点等等。