模糊逻辑

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第106页（1970字）

模糊逻辑一般地是在Lukasiewicz多值逻辑系统上构造起来的。

不仅如此，模糊逻辑还为刻画自然语言的实际推理构造了模糊语言值逻辑的新内容。一般认为模糊逻辑包含多值逻辑与语言值逻辑那部分。根据B、R、Gaines的分类〔1978〕模糊逻辑常在以下三种意义下被使用着

(1)把L、A、Zadeh 1965年提出模糊子集论以前用日常语言进行推理的根据、全部称为“模糊逻辑。”

(2)把多值逻辑的全部或部分称为“模糊逻辑”。

(3)在允许包括t命题的意义下，对多值逻辑的拓广并进一步模糊化，也称之为与自然自然语言相关联的模糊逻辑。用FL特称它。

自然FL包含了语言值逻辑。

基于Lukasiewicz多值逻辑基础上的模糊联结词是在λ截集意义下进行的。

设P，Q为原始命题。P^λ，Q^λ表示对应P，Q模糊集的λ截集。则P^λ=〔P₁，P₂〕，Q^λ=〔q₁，q₂〕对应了一个λ截集(闭区间)。此时：FL下的逻辑联结同

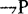(否定)对应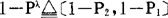

P∧Q(合取)对应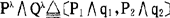

P∨Q(析取)对应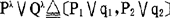

P→Q(蕴涵)对应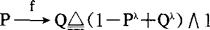

=〔(1－P₂+q₁)∧1，(1－P₁+q₂)∧1〕

以上的讨论是静态的(在固定的λ∈〔0，1〕程度上讨论)。

结果都是与λ有关的截集。当λ变化时，这些截集也随入变化，因此，逻辑运算的结果是一个随入而变化的具有弹性边界的区间。在上述意义上，我们常常讲，某命题是λ－真的。(无论是初始命题，复合命题还是逻辑演算的结论)

为了刻画自然语言的逻辑关系，在FL中不能象多值逻辑那样，命题的真实程度用〔0，1〕区间上的确定值来描绘。

必须要用模糊集来描绘。换句话说：一个自然语言命题的语言真值是真值论域〔0，1〕上的模糊子集。

为此，L，A，Zadeh给出了基本语言真值的定义；从而创立了语言值逻辑。

基本语言真值true(真)和fa1se(假)定义为

等式的左端是模糊集“真”上u命题的隶属度，

等式的右端是命题u在真值论域上的语言真值。

我们可以把它叙述为命题u在“真”模糊集上的语言真值就是u属于该模糊集上的隶属度。而同一个命题u在“假”模糊集上的语言真值就是用1减去它在“真”模糊集上的语言真值。

此外，同样的方法可以给出另外三个：

它们分别叙述为：

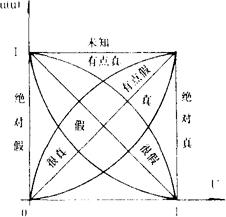
命题u只有当它是绝对真(绝对假)时，给它相应的语言真值为1，否则均为0。最后一个式子可以理解为，对任一命题u讲它是“未知的”总是允许的，对这种的说法，我们赋予它的语言真值是1。

当对基本语言真值加以修饰时，如“很”，“有点”“相当”等，语言真值会有变化：

设τ是某语言真值，很“τ″，有点“τ”可定义如下：

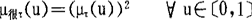
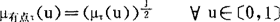
上式可叙述为，对语言真值只有τ的命题讲它很τ其语言真值反而下降了。(∵(μ_τ(u))²＜μ_τ(u))相反，讲它有点τ则上升了。

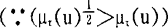
数学化地使用修饰词，可有如下的结果：

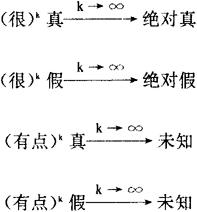
这与人们直观的理解与表述是相吻合的。

如上数量化的表述可隶属度——真值论域=继平面上的图形刻画。