变分法
书籍:方法大辞典
出处:按学科分类—自然科学总论 山东人民出版社《方法大辞典》第220页(753字)
是解薛定谔方程的一种近似方法。
因为薛定谔方程为一偏微分方程,除几个简单体系外,大多数体系的薛定谔方程不能精确求解,所以要用近似方法求其近似解。
对于薛定谔方程
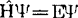
若已知其波函数ψ,则用ψ*乘以上式两端且积分可得体系能量
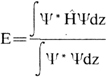
对于一个坐标q的函数Φ(q),一般地讲,Φ(q)不是上述方程的解,但我们总可以计算下列积分而得到数W
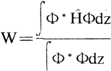
W与体系能量E有着密切的关系。可以证明,对于满足波函数三个标准条件的任一函数Φ,按上式计算得到的W一定不小于体系的基态能量E。
这称为变分原理。
根据变分原理,我们可以选择一系列函数Φ1,Φ2,…,求得相应的W1,W2,…,在这些W1中,最小的一个WJ一定最接近体系的基态能量E0,这个WJ就可认为是基态能量的近似值,而相应的ΦJ就可认为是体系基态的近似波函数,基于变分原理的这一方法就称为变分法。
为减少运算量,通常是先选择一个包含若干可供调节的参数C1,C2,…,Cn的函数中
Φ=Φ(x,y,z,c1,c2,…,cn)
代入前面式子求W,这样求到的W一定是参数C1,C2,…,Cn的函数
W=W(C1,C2,…,Cn)
然后再求当C1,C2,…,Cn为何值时,W最小,这样求到的C1,C2,…,Cn代入Φ和W中,就可得到体系基态的近似能量和波函数。
这样,一次就可在一种类型的函数中选择出最佳的近似波函数。包含若干参数的函数Φ称为变分函数,这些待定的参数C1,C2,…,Cn称为变分参数。