闭回路法

出处：按学科分类—经济 中国财政经济出版社《中国物资管理辞典》第504页（946字）

对物资调运问题的方案进行检验及改进的一种方法。

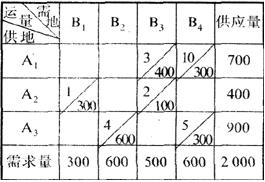
所谓闭回路，即选任一没有填数字的空格作为出发点，沿水半方向(向左或向右)前进(在前进过程中，可穿过填有数字的方格或空格)，遇到一个合适的填有数字的方格，即转向沿垂直方向(向上或向下)前进，按此走行规则，转向多次后，回到原出发点，形成一条闭回路。在这条闭回路上的转向方格称为顶点，除作为起点的顶点方格没有填数字以外，其余的顶点在方格内都必须填有数字。从起点开始，沿闭回路前进，将奇数顶点的运费(元／吨)取负值，将偶数顶点的运费(元／吨)取正值，然后相加，求代数和，就是这个起点空格的检验数。仍以最小元素法所举实例(初始调运方案)说明，选从(2，4)空格出发，经填有数字的(2，3)，(1，3)和(1，4)方格，又折返(2，4)空格。

在这条闭回路中，把奇数顶点的运量各减少一吨，而将偶数顶点的运量各增加一吨，即将初始方案中由A₂调往B₃，改为由A₂调往B₄，为保持新的平衡，在(2，3)处减少一吨物资，(1，2)处增加一吨物资，(1，4)处减少一吨物资，经这样调整，运费变化为(2，4)处增加8元，(2，3)处减少2元，(1，3)处增加3元，(1，4)处减少10元，结果为λ₂₄=8－2+3－10=－1，即减少一元，因此，这样调整是合算的。将数字－1填入(2，4)空格，称为空格(2，4)的检验数，这相当于单纯形解法中计算非基底变量的C₁－Z值。

每个空格存在唯一的闭回路，所有空格的检验数构成检验数表。如所有检验数都是非负值，相应调运方案一定是最优的，否则不一定最优，需选择负检验数绝对值最大的空格对运量进行最大可能的调整。在本例中，(2，4)空格检验数λ₂₄=－1，为使A₂物资调往B₄，需减少A₂运往B₃和A₁运往B₄的运量，选X₂₄=min｛X₂₃，X₁₄｝=min｛100，300｝=100，进行新的平衡：X₂₄=100，X₁₃=500，X₁₄=200，经这样调整后，所有检验数没有一个是负数，就达到了最优解。

经改进的方案比原方案节省的运费△S=100×1=100元。

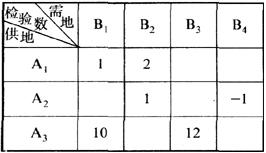
初始调运方案

检验数表