整数规划

出处：按学科分类—经济 经济科学出版社《企业管理学大辞典》第552页（976字）

变量只能取整数值的线性规划方法。

例：有一个背包，其总容量为10公斤，若有以下一些物品可以装入背包中，问如何装使得背包中物品的价值最大?

物品 A₁ A₂ A₃ A₄ A₅ A₆

重量(公斤) 1 0．3 0．8 2 0．1 3

价值(元) 10 4 6 15 2 25

解：设在背包中分别装入了物品A₁，A₂，A₃…A₆各为x₁，x₂，x₃…x₆个，则据题意：

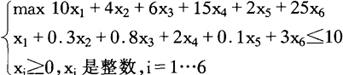
整数规划问题是实际工作中常见的问题，因为决策中所碰到的决策变量有许多都是只能取整数的，如生产产品的产量，投入工作的人数，等等。整数规划就是处理这类决策问题的规划方法，它同线性规划惟一的区别就在于其约束条件中多了对部分或全部决策变量为整数的限制。多了这一点限制之后，线性规划的单纯形法就无法使用了，为了求解整数规划问题，则只能采取穷举法或动态规划的方法。动态规划的方法运用起来比穷举法能少一点运算量，然而比起相同规模的线性规划问题，整数规划的描述力很强，可以运用于多种领域的问题中，如生产计划、车间调度、工厂选址、运输后勤、投资计划等领域中。

这里有一个运用整数规划的例子。艾尔福德有限公司是一家生产照相器材的英国公司，该公司在最终产品的生产过程需要使用若干种中间产品。由于生产时间的不同，不同批次的中间产品的某些化学性质会发生变化，为了生产出高质量的产品，必须把这些不同批次的中间产品适当地配合使用。过去，这种协调工作是由公司公共部门中经验丰富的工程师来完成，需要六个人干一周，一旦中间有什么差错，就会使生产受到耽误，造成损失。

自从公司将这个协调问题由外部咨询人员制成整数规划模型，并编制出程序放在计算机上运行之后，所有的工作(包括编制、保存、更新记录在内的文书工作)由一个普通的技术人员不到一天就可以完成，因此极大地提高了生产效率，降低了成本，同时原先总会出现的故障也少得多了。