BCI－代数

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第17页（3715字）

由日本井关清志在1966年引入，以集合论、命题演算、群论、Boole代数等为背景。

经过20多年的发展和国际上一批数学工作者的努力，尤其是一些中国数学工作者的突出工作，使得BCI－代数已成为当前国际上比较活跃的一个抽象代数分支。

BCI－代数实际上是一类泛代数。一个BCI－代数是具有下列条件的(2，0)型的(泛)代数＜X；*，0＞：

I－1．((x*y)*(x*z))*(z*y)=0，

I－2．(x*(x*y))*y=0，

I－3．x*x=0，

I－4．，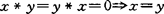

I－5．．

它可如下地引入自然半序：

I－6．

20世纪60年代以来，BCI－代数的发展过程大体上可以分为两个阶段。

第1阶段是1966～1979年。

在这1阶段中BCI－代数理论的最大成就是井关清志等人引入了BCI－代数和BCK－代数(BCI－代数的一种特殊情形)的概念。在第一阶段中对BCK代数的研究得到初步发展。

日本、波兰、苏丹和斯里兰卡的20多位作者写出了几十篇有关BCK－代数的论文，对BCK－代数从性质、若干类、生成新代数的方法及子集(包括理想)等方面进行了较为系统的研究。尤其是井关清志和塔那加等人在这一阶段中作了很多很好的工作，引进了许多概念，得到了一批有意义的结果，对可换性、有界性、拟可换性、关联性、正定关联性及具有条件(S)的性质进行了较系统的研究，开拓和丰富了BCK－代数的研究工作。

第2阶段是从1980年至今。

在第1阶段中除了BCK－代数的一些结果外，BCI－代数的研究工作并没有多大进展，这是因为BCK－代数类代数类。1980年井关清志肯定地得出结论，给出了第1个真BCI－代数的例子，并对BCI－代数进行了一些初步的研究。

1980年以来，中国数学工作者开始投入BCI－代数理论的研究工作，陆续写出和发表了一批论文，尤其是胡庆平在1987年出版了《BCI－代数》一书，这是国际上第1本关于BCI－代数的专着，给BCI－代数理论建立了一个框架。

中国数学工作者在这10多年中陆续研究和开拓了BCI－代数的一系列课题和专题方向，大大地推进了BCI－代数理论的研究。例如，1980年胡庆平和井关清志，引进了结合BCI－代数的概念，把BCI－代数和群论联系起来，且开拓了研究BCI－代数的一个方向：1985年，雷天德在此基础上引入了广义结合BCI－代数；1987年胡庆平和李欣，引入了具有散子代数性质的BCI－代数；1990年胡庆平，引入了具有散有限半序性质的BCI－代数。

这些代数类间有下列真包含关系：结合BCI－代数类广义结合BCI－代数类具有散子代数性质的BCI－代数类具有散有限半序性质的BCI－代数类代数类。

经过10多年的大量研究，现在已经发现BCI－代数与泛代数有密切的关系。实际上，BCI－代数是泛代数意义下的一种代数，也是具有代数结构和自然序结构的一种数学公理系统，因而也研究泛代数中一般研究的问题，例如簇论和理想等。关于簇论的结果已有：一切BCK－代数的类和一切BCI－代数的类皆是亚簇，可换BCK－代数类，(i，j；m，n)型拟可换BCI－代数类等都是簇。

在BCI－代数理论中对理想除了一般研究外，还利用理想成功地引入了商代数。

BCI－代数与格论、群论也有密切的联系。例如，我们已经知道BCI－代数理论中有下列结果：任意有界、可换的BCK代数是相对于∧和∨的一个格；一个BCK－代数在一定条件下成为一个Boole代数；胡庆平和井关清志(1982，1984)得到：如果BCI－代数＜X；*，0＞是结合的，则(X，*)是以0为恒等元的对合群，其逆亦真；雷天德进一步得到了广义结合BCI－代数和交换群之间的密切的“伴随”关系。

BCI－代数与点集拓扑和拓扑群也有密切关系。一个BCI－代数＜X；*，0＞再赋以拓扑结构，且使*成为连续映射，就成为BCI－拓扑代数，由自然半序引入的自然拓扑等都可满足这一条件，这种拓扑代数和拓扑群有密切的关系。另一方面，胡庆平(1987)还研究了BCI－代数的拟一致结构和一致结构，进而引入了一致拓扑，从而赋以拓扑结构。

这10多年中BCI－代数理论研究的主要方向是：(1)纯代数的研究。即BCI－代数理论的内在数学研究，主要着力于以下几个方面：本身性质的研究，构造新代数的方法探讨，各类BCI－代数的结构研究以及基数问题、真类问题及真子类问题的研究，结合性－广义结合性－具有散子代数性质这一方面的研究，子集和点的研究。

(2)与其它数学分支联系的研究。即BCI－代数理论的外部的数学研究，主要是BCI－代数与泛代数、格论、群论、点集拓扑和拓扑群等分支的联系，还有与集合论、环论、根性理论等方面的联系，都已有人展开一些工作，分别取得了一些结果。(3)建立和提出一些新的课题，使BCI－代数理论的研究不断深入，如胡庆平(1988)研究BCI－代数自然半序的几何特点，和研究了用自然半序定义的一类代数——具有散有限半序性质的BCI－代数，这实际上开拓了BCI－代数理论研究的一个新课题——BCI－代数自然半序的序结构研究(1990)。

从目前来看，BCI－代数理论研究的重点专题主要有：(1)BCI－代数的自然半序。

主要首先研究极小元，胡庆平和胡志刚已经得到了极小元定理、极小元乘积定理和链积问题等一批结果，进一步应对原子、高层元素、整个自然半序结构等展开深入的研究。(2)几类BCI－代数。对拟可换的BCI－代数、类拟可换的BCI－代数、具有条件(S)的BCI－代数、正常的BCI－代数和局部有限的BCI－代数等分别进行了一些研究，已取得一批结果。(3)扩张问题。对BCK－代数扩张为BCK－代数、BCK代数扩张为BCI－代数、BCI－代数扩张为BCI－代数等均已有所研究，并也有一些有趣的结果。(4)BCI－代数的范畴BCI。

研究其一些性质、有关的几个问题及子范畴等，已取得一些研究成果。(5)BCI－代数的同调。

已对BCI－代数的链复形、同调代数及同伦等问题展开了研究，得到了一些结果。(6)环式BCI代数。

已引入了环式BCI－代数的概念，研究了环式BCI－代数的一些性质，并利用矩阵方法，研究环式BCI－代数的其它问题。(7)BCI－拓扑代数。

对其一些代数问题、拓扑问题及进一步的问题已分别进行一些研究，已有一些初步的结果。(8)BCI代数理论的应用。已经在泛代数、群论和数论等分支中找到一些应用、得到一些成果。

。

【参考文献】：

1 Imai Y,Ieski K. On axiom system of propostional calculi. Proc Japan Acad, 1966,42:19～22

2 Iseki K. Proc. Japan Acad, 1966,42:26～29

3 Hu Qingping, et al. Math.Zem Notes,1980,8:553～555

4 胡庆平，等．科学通报，1982，12∶714～716

5 Hu Qingping et al．Math，Jap，1984，2∶251～253

6 胡庆平．BCI－代数．西安：陕西科学技术出版社，1987

7 胡庆平，等．纯粹数学与应用数学，1987，1∶39～46

8 胡庆平．数学杂志，1987，1∶63～69

9 胡庆平．西北大学学报，1988，3∶5～8

10 胡庆平．纯粹数学与应用数学，1990，2∶13～20

(西北大学胡庆平教授撰)