相似理论和相似比
出处：按学科分类—工业技术 企业管理出版社《工程师手册》第270页（3859字）
解决相似问题的关键是找出相似系统各尺寸参数的相似比。在基本相似条件和相似三定律的基础上，可引出求相似比的各种方法。
1．基本相似条件
(1)相似
一组物理过程其基本参数之间有固定成比例的数量关系称为相似。
(2)基本相似比
互相独立的基本物理量长度L，力F，时间T，温度θ，电量Q等形成的相似比为基本相似比，其中长度、力、时间为基本量纲。
(3)导出相似比
根据量纲理论，某些参数量纲由基本参数量纲导出，其相似比称为导出相似比，如速度、加速度的相似比。
(4)系统相似
长度相似比
φ1l2／l1=d2／d1=k2／k1=……
①几何相似 系统中各对应长度(l、d、k…等)成比例，各对应角相等，称为几何相似。
②力相似 几何相似的系统各对应点力方向一致，大小成比例(即力场几何相似)，称为力相似。
③运动相似 几何相似的系统各对应点上速度、加速度方向一致，大小成比例(即速度场、加速度场相似)，称为运动相似。
各物理量及系统相似的条件及相似比列于表2．3．2－1。
表2．3．2－1 物理量的相似
2．相似三定理
相似理论的基础是相似三定理。1868年法国J．Berfrand提出相似第一定理，指出了彼此相似的现象应具有的性质。1914年美国J．Buckingham提出相似第二定理，分析了相似现象各物理参量的表达。1930年苏联M．B．KHPИHIIEB提出的相似第三定理引出物理现象相似的充分必要条件，标志着相似理论的进一步完善。
相似三定理表达如下：
(1)相似第一定理(相似正定理)：彼此相似的现象必定具有数值相同的同名相似准则，且相应的相似指标为1。
(2)相似第二定理(П定理)：一个物理系统有n个物理量，其中k个物理量的量纲是相互独立的，则物理量可表示为(n－k)个相似准则П1、П2……Пn－k的函数关系：
f(П1、П2、……Пn－k)=0
(3)相似第三定理(相似逆定理)：对同一类物理现象，如果单值条件(几何条件、介质条件、初始条件、边界条件)相似，由单值条件的物理量所组成的相似准则在数值上相等，则现象相似。
3．相似准则和相似指标
各种物理现象根据其物理关系式可推导出由物理量组成的无量纲数群，它在该现象的不同点上具有不同数值。当两现象相似时，在对应点上有相同数值。此无量纲数群即为相似准则。
与相似准则各参数对应的相似比组成的关系式称为相似指标。两现象相似，其相似指标等于1，这是相似现象对各参数相似比数值间的约束指标。
如分析质点运动系统，物理关系式v=l／t、其相似准则是无量纲数群vt／l，而相似指标是φvφt／φ1。
(1)简单系统可直接由物理关系式求相似准则和相似指标。如惯性系统其主要物理关系为牛顿第二定律
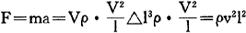
F／ρv2l2就是系统中惯性力F、密度ρ、速度v及长度l等基本参数组成的无量纲数群，称为牛顿准则。
当两惯性系统相似，存在φF=F2／F1，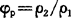
，φv=v2／v2，φi=l2／l1，物理关系式：
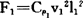①
F2=Cp2v22l22 ②
式中C为比例常数。
②÷①】 ③
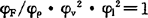，相似准则为1。
③代入物理参数
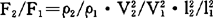
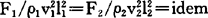，相似指标相等。
(2)复杂系统要从几个物理关系式求有关的相似准则。如流体系统主要受三种力作用：
惯性力 Fa=ma△ρv2l2
重力 Fg=mg△ρl3g
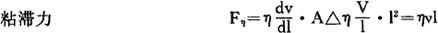
式中l－长度(或直径)，ρ－介质密度：η——介质粘度：v－流速，g－重力加速度。
定义雷诺数Re为惯性力与粘滞力之比，付鲁德数Fr为惯性力与重力之比
Re=ρv2l2／ηvl=ρvl／η
Fr=ρv2l2／ρl3g=v2／gl
用雷诺数可判断流体状态。Re≤2000为层流，而Re＞2000则为紊流(湍流)状态。
在流体系统的相似分析中粘滞力起主要作用时用雷诺准则，而重力起主要作用时用付鲁德准则。
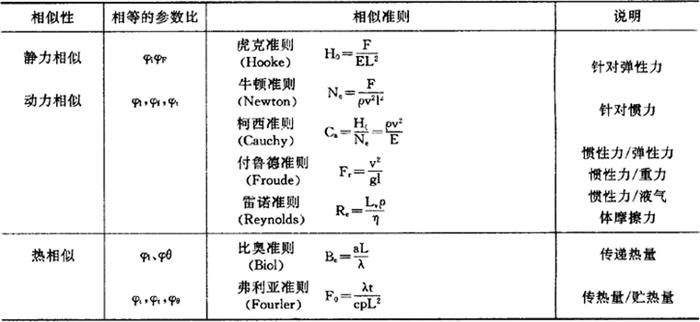
各工程领域都有一些重要的相似准则，见表2．3．2－2。
表2．3．2－2 常用的相似准则
(3)当系统比较复杂，无法用一个相似准则说明问题时，可以用相似第二定理(П定理)决定所需相似准则的数量。
4．相似比方程
解决相似问题的关键往往是求各参数的相似比。在相似三定理的基础上可用方程分析法，量纲分析法等求相似比方程，再解方程即得相似比。
(1)由相似准则求相似比方程
(2)方程分析法
由参数关系式求相似比方程。系统的物理或几何参数关系式可表达为：
A=CXmYnZp
式中 A－因变量参数；
C－常数；
X，Y，Z——自变量参数；
m、n、p——指数，可为任意实数。
相似系统存在相同的参数关系式及相应的参数比。
φA=A2／A1，φx=X2／X1，φY=Y2／Y1，φz=Z2／Z1
A1=CX1mY1nZ1p ①
A2=CX2m／Y2n／Z2p ②
②÷①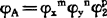
两系统相似时，其相似比方程式中各参数相似比对应于参数关系式中的参数，而常数不出现。
(3)量纲分析法
量纲分析是“物理对应”的设计方法，而量纲是通过基本度量单位表示导出单位的表达式。物理量的基本度量单位只有三个，即长度L，时间T及力F(或质量M)，任何力学物理量都可由这三个基本度量单位表达，如表2．3．2－3。
表2．3．2－3 常用物理量的量纲表达
*[0]=[F°L°T°]材料密度ρ(g／mm2)及弹性模数E[N／mm2→(kg·m／sec2)／mm2]有关。
F(f，l，ρ，E)=0
根据物理关系式方程等号两边量纲齐次的原理，可推算出指数未知的物理方程。