模拟试验与相似理论

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第371页（1918字）

有些工程技术对象，不便于或不允许进行直接试验，需要建立与之相似的模型，通过在模型上进行试验，获得规律性的认识，然后再把这些认识推广到实际研究对象上去。这种通过模型间接地认识原型的试验研究方法，就叫做模拟试验。这里，模型是模仿被研究对象而设计出来的某种物理装置、电路或电子模拟计算机，原型是现实存在或预期制造的工程技术产物，是被研究的对象。

模拟试验分物理模拟和数学模拟两种。物理摸拟的理论基础是相似理论，相似理论是二十世纪三、四十年代形成和发展起来的，它的主要内容是三个相似定理。下面，扼要介绍一下三个相似定理的内容。

1．相似概念和相似常数

物理相似包括几何相似和各种物理量相似。

几何相似指的是，若两个系统有互相对应的部分，且所有对应的尺寸成比例，则称它们是几何相似。譬如两个三角形相似，指的是它们的对应边成比例，即：

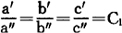
其中C₁为比例常数。

各种物理量相似是指，两个系统中对应的矢量在方向上相应地一致，在数值上相应地成比例；标量在对应的空间点上和时间间隔上相应地成比例。譬如动力相似，是指两个系统在对应点和对应时刻，所受的力互成一定的比例。即：

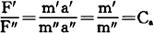
该式表明，在加速度互成比例C_a的运动相似系统内，只要对应的质量互成一定的比例，则两个系统的动力便相似。

2．相似第一定理

相似第一定理是由别尔特朗确立的。该定理表述为：凡彼此相似的现象，必定具有数值相同的相似准则。

以动力相似为例。根据相似概念和牛顿第二定律，如果两个动力系统相似，它们必服从微分方程(F表示力，m表示质量，w表示速度，t表示时间)。描述两个系统的方程为：

由于两系统相似，则各对应量成比例，即：

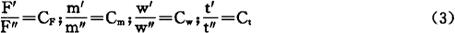
式中，C_F，C_m，C_w，C_t为比例常数。

将式(3)代入式(2)，得

现将式(4)作进一步转换，把式(3)代入式(4)，得

在这两个系统间数值都相同的这一综合量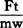，即是所谓相似准则。如果两个系统相似，必须具有数值相同的相似准则。相似准则给我们带来很大方便。由于它在相似系统中数值相同，因而在模拟试验中，能够把在模型上得到的相似准则推广到原型上去。

3．相似第二定理

相似第二定理是俄国人费吉尔曼和美国人布海金提出来的。其内容是：当一现象由n个物理量的函数关系来表示，且这些物理量中含有m种基本量纲时，则能得到(n－m)个相似准则；描述这一现象的函数关系式，可表示成(n－m)个相似准则间的函数关系式。其表达式为：

F(π₁，π₂，……，π_n－m)=0 (6)

式中，π₁，π₂，……，π_n－m为相似准则。

相似第二定理亦称π定理，它告诉我们如何整理试验结果，使在模型上所得到的试验结果能推广到原型上去。

4．相似第三定理

相似第三定理是前苏联人基尔皮契夫创立的。其内容是：凡具有同一特性的现象，当单值条件(系统的几何性质、介质的物理性质、起始条件和边界条件等)彼此相似，且由单值条件的物理量所组成的相似准则在数值上相等，则这些现象必定相似。

相似第三定理是第一定理的逆定理，它给出了现象相似的充分必要条件。