物理模拟

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第373页（1940字）

物理模拟是以模型和原型之间的物理相似为基础的模拟方法。

物理模拟的基本步骤是：

1．根据相似第三定理制造模型；

2．在模型上试验，测取数据；

3．根据相似第三定理把试验结果推广到原型上去。

下面举例说明物理模拟的基本步骤。

例如，如图4．5．6－1所示，有一个物体，仅受一个弹性恢复力作用而运动，试通过试验认识其规律

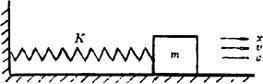
图4．5．6－1

第一步，是制造模型。在制造模型之前必须先求出相似准则。求相似准则的方法很多，有方程分析法、量纲分析法等。这里采用量纲分析法。

由分析可知，本系统可用下述物理量表征：速度(v)，加速度(a)，质量(m)，位移(x)，时间(t)和弹性元件的刚性系数(k)。则描述该系统运动规律的一般函数关系式为：

f(v，m，x，t，α，k)=0 (1)

式(1)可展开为幂级数。展开后，根据物理方程式的量纲齐次原则，用幂级数中任一项除其他各项，得到的幂级数则是由无量纲的项所组成的。每个无量纲的项都称作π项，其中一般的π项形式为

π=v^αm^βx^γt^δα^εk^τ (2)

写出π项中各物理量的量纲，则(2)表示为：

π=[LT^－1]^α[FT²L^－1]^β[L]^γ[T]^δ[LT^－2]^ε[[FL^－1]^τ (3)

式中，F、L、T分别为力、长度、时间的基本量纲。

整理式(3)，得

π=[F]^β+τ[L]^{α－β+γ+ε－τ}[T]^{－α+2β+δ－2ε} (4)

因为π项为无量纲项，则使式(4)中量纲F、L、T的指数为零，得到

只要在α、β、γ、δ、ε、τ中给定三个变量的值，便可由式(5)解出另外三个变量值。把每组变量值代入式(2)，便获得许多π项，其中独立的只有(n－m)即6－3个，这些独立的π项即为相似准则(证明略)。本例得到的三个相似准则为π₁=kt²／m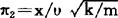；；π₃=αt²／x。

有了相似准则，便可以制造模型了。依相似第二定理，模型与原型相似必须有

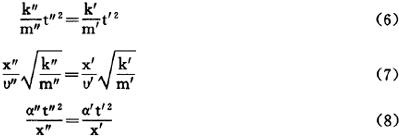
式左端为模型的相似准则，右端为原型的相似准则。假如希望模型与原型的时间相似倍数】，位移相似倍数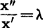，则代入式(6)、式(7)、式(8)得到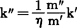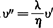；′；。可见，给出不同的相似倍数，将会得到不同的模型试验条件，从而使模型具有所希望的便于试验的形状。依模型试验条件，便可制造模型。

第二步，是在模型上进行试验，测得多组试验数据，获得许多组t″、x″、υ″和α″的值。

第三步，是处理试验数据，推广试验结论。

依相似第三定理，这里所研究的系统的运动规律可由F(π，π₂，π₃)=0来描述。该式还可改写为下述形式：

π₂=f₂(π₁) (9)

π3=f₃(π₁) (10)

π₂、π₃的具体函数形式能由测得的试验数据得到。将每组试验数据t″、x″、υ″和α″代入相似准则式π₁=k″t″²／m″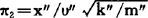，，π₃=α″t″²／x″，便求出多组π₂与π₁的对应值。每组π₂与π₁的值可描一点，这些点的连续曲线就是π₂与π₁的函数关系。同理，将每组π₃与π₁值描一点，这些点的连续曲线便是π₃与π₁的函数关系。根据相似第一定理，模型与原型的相似准则数值相同，则它们的相似准则函数关系式也必是相同的。因此，可以把模型试验得到的结果直接推广到原型上去。