线性规划法

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第443页（670字）

例 某企业生产两种产品，甲产品每台利润50元，乙产品每台利润90元，有关生产用的资料如表2．5．1－1所示，试求当企业利润额最大时两种产品的产量。

表2．5．1－1 甲、乙产品生产用资料

解设 x₁——甲产品的生产数量

x₂——乙产品的生产数量

F(x₁)——企业利润函数 i=1，2

目标函数 maxF(x_i)=50x₁+90x₂

可以用运筹学中的单纯形法求解，也可以用图解法。此处仅以图解法说明优化过程：

以x₁，x₂分别为横坐标和纵坐标，然后作出约束方程所描述的约束线，如图2．5．1－1中①，②，③直线所示，又因为x₁，x₂均大于零，因此可得到图2．5．1－1中阴影部分所示的可行解区域。

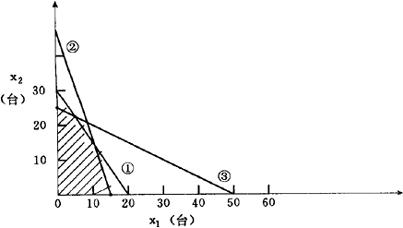
图2．5．1－1 线性规划图解

可以证明，目标函数的最大值一定在此可行解区域的凸点得到，由此可以通过计算得到，四个凸点中使目标函数达到最大值的点是x₁=5，x₂=22．5，即当生产甲产品5台，乙产品22．5台时企业获得的利润最大，为2275(元)。