不确定性分析

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第676页（5380字）

对方案进行技术经济分析时，所用的基础数据如投资、售价、产量、成本等都是通过估计、预测获得的。实际上，经济活动的各项因素总是在不断变化的，上述估计、预测的数据是不可能和未来的实际情况完全相符合，这样就构成了对方案评价的不确定性，从而导致最终选择的方案具有一定的风险性。

为了提高方案经济评价的可靠性，提高决策的科学性，需要对方案作不确定性分析。尤其对投资数额大、寿命长的项目，不确定性分析更为重要。

不确定性分析的主要方法有盈亏分析和敏感性分析。

1．盈亏分析

盈亏分析又可称为量本利分析，它是通过运用代数计算和图示分析的方法，来研究产销量、成本、利润三者之间的关系以及对盈利或亏损的影响，并根据盈亏状况及其经营安全状况来评价方案的优劣。

(1)线性盈亏分析

企业产品成本总额由固定成本总额和变动成本总额组成，即：

C_m=C_f+C_v=C_f+C′_vQ

式中，C′_v——单位产品变动成本。

企业产品成本总额和产量的关系可用图2．3．3－1来表示。

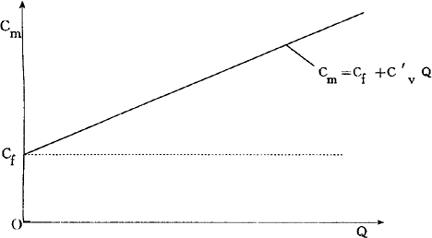
图2．3．3－1

产品销售收入是产品销售量和单位产品价格的乘积。在供小于求且价格稳定的市场条件下，产品销量可以和产品产量等同看待，单位产品价格亦是常量。这样，销售收入就是产品产量的线性函数，即：

S=S_aQ

式中，S_a——单位产品的销售价格。

销售收入与产销量的这一线性关系如图2．3．3－2所示。

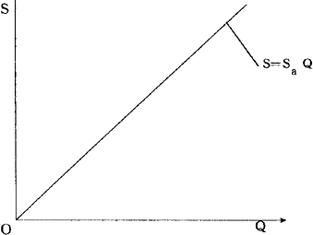
图2．3．3－2

把产品成本－产量图与销售收入－产销量图画在同一个图上即得盈亏分析图2．3．3－3。

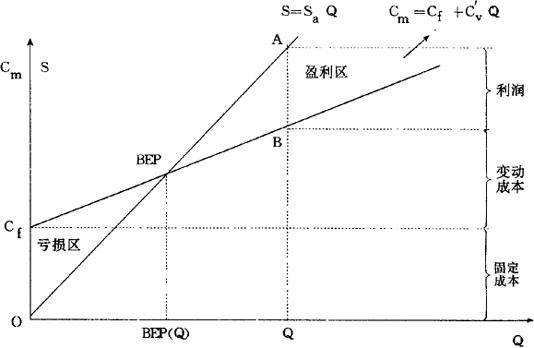
图2．3．3－3

盈亏分析图是盈亏分析的重要组成部分，它直观地表示了产品产销量、成本、利润之间的关系。

在图2．3．3－3上，销售收入线OA与产品成本线C_fB线并于BEP点，BEP点将两直线所夹的区域分成两部分，BEP点左边的成本线高于销售收入线，为亏损区；BEP点右边的销售收入线高于成本线，为盈利区，BEP点为盈亏分界点，该点销售收入等于产品成本总额，利润为零。因此，称BEP点为盈亏平衡点。

当产品实际产销量大于平衡点产销量时，项目获利，反之，就会亏损。盈亏值可根据图2．3．3－3中产品销售收入线与产品成本总额线的纵座标差求得。

用代数方法亦可以求盈亏平衡点。

销售收入为：S=S_a·Q

产品成本总额为：C_m=C_i+C′_vQ

根据盈亏平衡点的定义，有：

S=C_m

则：S_aQ=C_f+C′_vQ

上式中的Q，就是以产销量表示的盈亏平衡点，用BEP(Q)表示，则

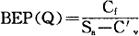
当产品产销量Q大于BEP(Q)时，项目能获利。

通常还可以用生产能力利用率来表示盈亏平衡点。

将求得的盈亏平衡点产销量与设计生产能力的产量(用Q_o表示)相除，即为盈亏平衡点的生产能力利用率，其表达式为：

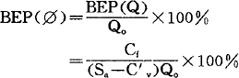
式中，BEP()——盈亏平衡点处的生产能力利用率。

盈亏平衡点产销量与盈亏平衡点生产能力利用率低，则表明项目抗风险能力强。

需要指出，在实际工作中确定盈亏平衡点时，往往除了产品成本总额外，还应考虑税金作为必要的支出。包括销售税金的盈亏平衡点计算公式为：

以实际产销量表示

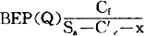
以生产能力利用率表示：

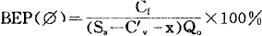
以上两式中，

x——单位产品销售税金。

(2)非线性盈亏分析

以上进行盈亏分析时，把产品成本总额和销售收入均视为是产销量的线性函数。但在现实中，产品成本总额、销售收入与产销量的关系均不一定都呈线性关系。

在有竞争的市场条件下，产量受销量的限制而销量的大小又主要取决于市场行情及竞争力。随着产销量的增加，企业有时为了扩大销售而降低价格，从而使销售收入线表现为曲线或折线。

单位产品变动成本往往也会随着产量的变化而变化。如，随着产量的逐步增加，机械化、自动化设备的比重加大，从而降低了单位产品的原材料消耗、减少了废品、次品，单位产品变动成本可能有所下降。但是，当产量超过生产能力正常利用程度时，又可能带来维修费用增加、废次品率上升等不经济因素，造成单位产品变动成本逐步增加。因此，变动成本与产量也往往呈曲线或折线关系。

一般来说，固定成本只能在一定的产量区间内保持不变。当产品产量增加到一定程度时，就要增添设备，扩建厂房，从而导致固定成本增加。因此，固定成本常常是随产品产量的增加而阶梯式递增。

产品产销量与成本、销售收入一般不会严格呈线性关系。如果它们之间的实际情况与线性关系相差很大，则应进行非线性盈亏分析。非线性盈亏分析图如图2．3．3－4所示。

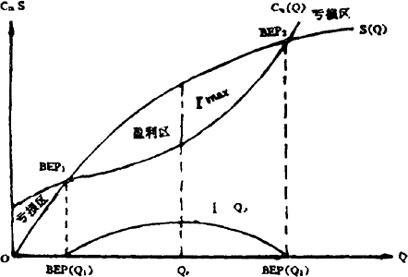
图2．3．3－4

图中，C_m(Q)曲线表示产品成本与产量的关系；S(Q)曲线表示销售收入与产销量的关系；C_m(Q)与S(Q)有两个交点BEP₁和BEP₂，这两个交点就是盈亏平衡点，对应的产量就是盈亏平衡点产量BEP(Q₁)、BEP(Q₂)。当产量Q小于BEP(Q₁)或大于BEP(Q₂)时，销售收入低于产品成本，因而出现亏损；产量Q在BEP(Q₁)和BEP(Q₂)之间时，企业盈利；而当产量Q等于Q_g时，取得的利润最大。

现求Q_g点，利润计算公式应为：

I(Q)=S(Q)－C_m (Q)

对上式两边求导并令M_m的导数为零，则：

I^’(Q)=S’(Q)－C’_m (Q)=0

得：S’(Q)=C’_m(Q)

由上式求得的产销量即为使利润最大的产销量Q_g。

2．敏感性分析

敏感性分析是一种常用的不确定性分析方法，其目的是要减少决策的风险。

例如，某投资项目预计需投资100万元，当年收益，每年净收益均为20万元，寿命10年，残值为10万元，基准收益率为10%。那么，其净现值为：

NPV=－100+20(P／A，10%，10)+10(P／F，10%，10)=26．7(万元)

该方案的净现值为26．7万元，显然是可行的，这是确定性分析。然而，实施以上方案并不一定就能盈利，因为方案因素是不确定的，方案具有风险，如果年净收益实际上没有达到预测值2万元，方案的经济效益就变差。假如年净收益只达到1万元，则NPV=－3．47(万元)，方案就不可行了。同样，如果寿命、投资、基准收益率、残值等发生变化，对结果也将产生影响。

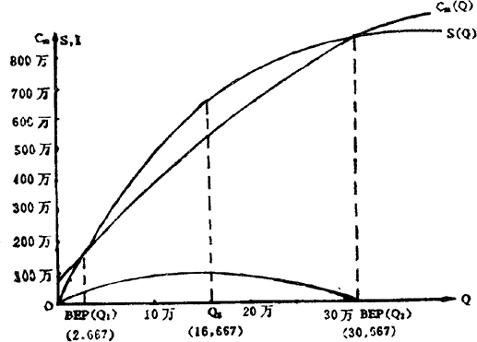
图2．3．3－5

敏感性分析的步骤如下：

(1)确定分析指标

方案的经济性是由净现值、净年值、投资回收期、内部收益率等指标加以反映的。实际上，不可能也不需要把每种经济效益评价指标都作为敏感性分析指标。只要选定一个或两个评价指标即可。但无论选定什么指标都应与项目评价指标相一致。例如，某方案所用的评价指标是净现值、内部收益率，则敏感性分析指标就只能是净现值或内部收益率。

(2)设定不确定因素

方案的不确定性因素主要有销售收入、成本、投资额、寿命期、建设期等。以上一些不确定因素又可进一步分解为若干个更具体的不确定因素，如：销售收入可分为销售量与售价这两个不确定因素；产品成本中的原材料费、燃料动力费等很显然是不确定因素。

敏感性分析并不要对方案所有的不确定性因素都进行逐个分析。一般预计未来变化不大不确定因素(可近似认为是确定性因素)及可以肯定是非敏感的因素，都可以不必做敏感性分析。比如，残值这一不确定因素一般对方案没有太大的影响，尤其是在使用寿命较长、基准收益率较高的情况下，残值就更不敏感了。通常，可以不对残值作敏感性分析。

因此，在进行敏感性分析时，要根据方案特点，对预计为未来变化大且不能确定为非敏感因素者需逐个作敏感性分析。在一般情况下，投资额、建设期、产品销量、产品售价以及主要原材料、动力、燃料、价格等不确定因素都是敏感因素，应在它们中有选择地进行敏感性分析。

(3)计算不确定因素的变化对分析指标的影响程度，找出强敏感因素

首先，要做两个假设：第一，当计算分析某个不确定因素变化对分析指标的影响时，假定其他因素都是已确定的；第二，假定每个不确定因素变化的机率是相等的。

然后，对每个需进行敏感性分析的不确定因素都设定一系列的变化幅度值并逐个计算出分析指标相应的数值。

接着，将结果加以整理并采用图表的形式表示出各个不确定因素变化与分析指标相应变化的数量关系。

最后，通过对表中分析指标的变化程度或图中曲线斜率的分析，判断出严重影响方案经济效益的强敏感因素。

(4)作出敏感性分析结论

根据强敏感因素对方案经济的影响程度，判断方案的风险性大小，作出分析结论。

一般来说，最优方案应是风险性较小的方案。如果通过敏感性分析，发现原来确定性分析时所选定的最优方案，其风险性也小，那么这就增强了决策部门的信心；反之，如其风险性较大，就要重新考虑选择最优方案了。

敏感性分析的计算虽然不难，但特别繁琐，重复计算过程很多，对大中型项目需借助于电子计算机来完成。

尽管敏感性分析应用较为广泛，但仍有其局限性，它只能分析单个不确定因素对方案经济效益的影响，而不能就多个不确定因素进行综合分析，也不能明确地指明某个不确定因素变动对方案经济效益影响的可能性有多大。