磁感应强度及磁通的概念、单位及其复现

出处：按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第345页（4912字）

1．磁感应强度及磁通的概念和单位

为了表征磁场的大小，人们曾按“磁荷”的观点，定义磁场强度H为表征磁场强弱的物理量，即磁场是通过磁荷在磁场中受力的大小来确定的(磁的库伦定律)。自从认识了运动电荷是磁现象的根源之后，常用磁场对运动电荷或载流导线的作用来描述磁场，由此引入了磁感应强度B。磁感应强度的大小可以通过载流导体在磁场中所受的力的大小来确定：

F=I△s×B (6．6－1)

式中，s为长度，I△s为电流元。在我国的“量和单位”国家标准中，也是以(6．6－1)式来定义磁感应强度的。在计量领域，以磁感应强度B为描述磁场的基本物理量，许多国家均建立了磁感应强度基准或标准，开展磁感应强度的量值传递。

与用电力线描绘静电场一样，也可用磁感应线(磁力线)描绘磁场。磁感应线上任一点的切线方向和该点处的磁场方向一致。同时用磁感应线的疏密来表示磁场的强弱，磁场较强的地方，磁感应线较密，反之，磁感应线就较疏。

通过一给定曲面的总磁感应线数，称为通过该曲面的磁通量，用符号Φ表示，在“量和单位”国家标准中，磁通［量］用下式来定义：

式中A为面积，θ为dA的法线方向与该点处磁感应强度方向之间的夹角。由式(6．6－2)可看出，B在数值上等于与其方向相垂直的单位面积上的磁通量，因此，磁感应强度又可称为磁通密度。在国际单位制中，磁感应强度的单位是特［斯拉］(T)，磁通的单位是韦［伯］(Wb)，1T=1Wb／m²=1V·s／m²。

2．磁感应强度单位的复现

(1)利用通电的线圈复现磁感应强度单位量值

几何尺寸稳定的线圈可以作为高准确度的磁感应强度标准量具使用，如螺线管线圈和赫姆霍兹线圈。当它们与线圈电流的稳定和测量装置相结合，即可准确地复现磁感应强度单位量值。这类线圈一般是在线胀系数小、变形小的骨架上绕制单层或多层绕组而成，其线圈常数值(即通以单位电流时产生的磁感应强度)通过对线圈几何尺寸的精密测量计算得到，或由高一级的磁强计进行测量确定。如图6．6－1所示单层螺线管轴线上的轴向磁感应强度的计算公式为：

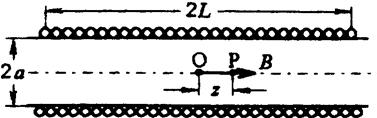
图6．6－1 螺线管线圈示意图

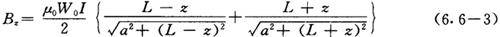
式中W₀为单位长度的匝数，I为线圈中通过的电流，z为轴线上所计算的点与中心点的距离。当电流和几何尺寸的单位分别为A和m时，磁感应强度的单位为T。当z=0时，即为线圈中心点的轴向磁场：

赫姆霍兹线圈是由两个同轴平行放置的、半径及匝数均相同的圆环形绕组构成，两绕组中心平面的距离等于绕组的半径(如图6．6－2所示)。这类线圈具有很高的均匀性，均匀区较大，很容易把被检仪器放入，因此在弱磁场范围内应用很广泛。赫姆霍兹线圈中心点轴向磁场的计算公式为

图6．6－2 赫姆霍兹线圈示意图

式中W₀为每个绕组的匝数，R为两绕组的平均半径。式(6．6－3)～(6．6－5)均为理想条件下的计算公式，实际的线圈由于对理想条件总有偏离，因此在准确度要求高时，实际的计算公式还必须包含各种必要的修正项。

采用精密线圈作为复现磁感应强度单位的基准器，其准确度可达到10^－7量级。我国采用两个赫姆霍兹线圈作为磁感应强度的基准器，其骨架为石英玻璃，上面磨有精密的螺纹沟并绕上镀金纯铜线(或无氧铜线)，导线的直径和绕组的直径及螺距等几何尺寸用激光干涉仪测定。计算得到的线圈常数值约为2．3×10^－4T／A，不确定度为5×10^－7，复现磁感应强度单位的不确定度为8×10^－7。

(2)利用质子回旋磁比γ′_p值复现磁感应强度单位量值

如6．3．1节的(6．3－4)式ω_p=γ′_p·B所示，当质子回旋磁比γ′_p的值准确测定之后，就可通过测量在磁场中的质子样品的共振频率来确定被测磁场的值。我国绝对测定的γ′_p值为2．6751541×10⁸S－¹T^－1，不确定度为8．6×10^－7，而频率测量一般很容易达到很高的准确度，因此，利用各种稳定的磁场源如线圈、电磁铁、超导螺管等与核磁共振磁强计一起即可组成不同量限的磁感应强度标准，准确度可达到10^－4～10^－6量级。我国用这种方法建立起从弱磁场到超导强磁场的四个不同量限的磁感应强度标准：10nT～1mT的弱磁场标准，0．1mT～50mT的中磁场标准，50mT～2T的强磁场标准和2～12T的超导强磁场标准。

3．磁通单位的复现

由6．2．2节中所介绍的互感的定义及本节前面介绍的磁通的定义可知，磁通Φ=MI或Φ=BA，所以它可以从磁感应强度和面积导出，也可以通过互感和电流来导出。我国是用后一种方法，即通过康贝尔线圈来复现磁通单位的。该线圈是由初级和次级两个线圈组成，初级线圈与赫姆霍兹线圈相似是由两个隔开一定距离的共轴的相同绕组构成，而次级线圈是与初级线圈共轴并位于初级两个绕组正中间的多层绕组(见图6．6－3)。如果初级线圈的螺旋线和次级一匝圆环之间的互感值为M₀，当次级线圈具有N₂匝时，该线圈的总互感将为M=N₂·M₀。M的值可通过对线圈的几何尺寸进行精密测量后计算得到。

图6．6－3 康贝尔线圈示意图

康贝尔线圈的计算准确度主要取决于初级的加工和测量准确度，而与次级的关系不大。这除了因为初级的两个绕组对称于次级外，还由于次级圆环刚好处在互感值对圆环的半径R₂最不敏感的地方。这就大大降低了对次级线圈的加工和测量准确度的要求，而且可以采用多层绕组增加匝数以获得较大的互感值。

我国用于复现磁通单位的康贝尔线圈其互感值约为0．01H(1H=1Wb／A)，不确定度为小于2×10^－5。除基准外，其它等级的磁通标准量具大多是由具有一定互感值的一系列精密互感器组成，常用标准量具的常数在10^－4～0．1Wb／A之间，年稳定性优于1×10^－4，不确定度通常为10^－4量级。

利用螺线管线圈和匝面积准确已知的测量线圈亦可构成磁通量具，用于复现磁通单位量值，不确定度一般为10^－3～10^－4量级。若螺管的磁场常数为K_B，测量线圈的匝面积常数为K_SW，则构成的磁通量具的磁通常数为

K_Φ=K_B·K_SW (6．6－6)

【参考文献】：

［1］国家技术监督局发布，GB3100～3102－93量和单位国家标准，中国标准出版社，1994年12月。

［2］王江主编，现代计量测试技术(第18章电磁计量技术)，中国计量出版社，1990年12月。

［3］程守洙、江之永主编，普通物理学第二册，人民教育出版社，1979年2月。

［4］俞大光编，电工基础，人民教育出版社，1958年9月。

［5］Г．И．阿塔别柯夫，线性电路理论，人民教育出版社，1963年12月。

［6］C．A．狄苏尔、葛守仁，电路基本理论，人民教育出版社，1979年1月。

［7］乔蔚川、刘瑞珉、沈平子，The Absolute Measurement of the Ampere by Means of NMR，IEEE Trans．Instrum．Meas．，vol．IM－29，No．4，Dec．，1980．

［9］张钟华等，NIM用计算电容测定的量子化霍尔电阻的SI值(英文)，计量学报，第16卷，第1期，1995年1月。

［10］刘瑞珉、刘恒基、金惕若等，NIM对γ′_p及2e／h的SI值的最新测定结果(英文)，计量学报，Vol．16，No．3，1995年7月。

［11］B．P．Kibble。I．A．Robinson and J．H．Belliss，A Realization of the SI Watt by the NPL MovingCoil Balance，CCE Documents 88－16，1988．

［12］P．T．Olsen。R．E．Elmquist，E．R．Williams，G．R．Jones and V．E．Bower，A Measurement of the NBS Electrical Watt in SI Units，CCE Documents 88－37，1988．

［13］Report of the 18th Meeting of CCE，1988．

［14］B．P．Kibble，I．A．Robinson and J．H．Belliss，The New NPL Moving Coil Balance-A Progress Report，CCE Documents 92－61，1992．

［15］唐统一、张钟华、张叔涵主编，近代电磁测量，中国计量出版社，1992年8月。

［16］袁楠、沈平子编，电磁量的单位制和单位的复现与传递，机械工业出版社，1986年4月。

［17］阮永顺、迈淑琴、王晓超编着，交流电桥检定与测试技术，中国计量出版社，1991年5月。

［18］唐佐梁、梁德正等，电能计量手册，河南科学技术出版社，1990年12月。

［19］K．J．Lentner．A Current Comparator System to Establish the Unite of Electrical Energy at 60 Hz，IEEE Trans．Instr．Meas．Vol．23，No．4，p．334－336，Dec．，1974．

［20］ю．B．阿法拉谢耶夫等着［苏］，张伦译，磁场参数测量器具，科学出版社，1983。

［21］p．Φ．阿克纳叶夫、Л．И．留必莫夫、A．M．巴纳休克－米罗维齐着，李绍贵，王登安译，电磁量计量器具的检定，中国计量出版社，1992年5月。