气体中的声速
出处:按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第548页(1993字)
距今整整300年前,即1687年,牛顿首先得出气体中声速
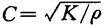
并根据波义尔定律推导出k=P.)为气体的压力。推导如下:
考虑一定质量的空气或其它气体,它的压力与体积分别为P与V,并令在一定的温度之下,发生很小的变化,即:
(P+δP)及(V-δV)
由波义尔定律: PV=常数 (11.2-1)
微分后有: PδV+VδP=0

而气体的弹性模量(这里指体积弹性模量)

比较(11.2-2)与(11.2-3)式即得到
P=k (11.2-4)
(式中负号表示,当压力增加时,体积减小)
当用牛顿的气体中声速关系 来计算0℃时的空气的声速,并用
来计算0℃时的空气的声速,并用
P=101.3kPa
ρ=1.29kg/m3
得C=280米/秒,它比实验数值低。
过了129年即1816年,拉普拉斯首先解释了这一偏离的原因。他指出,由于声波的压缩和膨胀如此迅速,会伴随有热量的得失,因而就会有温度的变化。而声波传播的速度又远大于热量传递的速度,声波传播的过程中来不及建立热平衡。条件是绝热的,而不是等温的,故应用波义定律是不对的。必须应用绝热方程。
PVr=常数
这里r是气体的定压比热对定容比热之比值(Cp/Cv)。
我们再对此进行微分就有:
rPVr-1δV+VrδP=0

与(11.2-2)相比得绝热的体积弹性模量=rP

应用上述同样的空气条件及r=1.40,就得出空气中的声速C为331.6米/秒,这就与实验值更为符合的数值,它沿用至今。
【参考文献】:
[1]IEC—327,Precision method for pressure calibration or one—inch standard condenser microphones by the reciprocity technique. 1971.
[2]1EC—486,Precision method for free—field calibration of one inch standard condenser microphones by reciprocity technique, 1974.
[3]IEC—150.Testing and calibration of ultrasonic therapeutic equipment, 1963.
[4]GB 3223-82,水声换能器的自由场互易校准
[5]GB 3785-83,声级计的电,声性能及测量方法
[6]GB 7341-87,听力计
[7]GB 7614-87,校准测听耳机用宽频带型仿真耳
[8]GB 7342-87,测听耳机校准用IEC临时参考耦合腔
[9]OIML R102,声校准器
[10]JJG 188-90,声级计
[11]JJG 698-90,积分声级计
[12]标准电容传声器有关国家标准及检定规程
[13]JJG 388-85,听力计