动态性能
出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第399页（2304字）
系统的动态性能可用时间域或频率域指标衡量，常用的时域指标有上升时间tr、峰值时间tp、调节时间te及超调量σp等。前三项指标可表明系统响应的快速性；超调量σp可表明系统响应的振荡程度，常用的频域开环指标有相角裕量γc和幅值穿越频率ωc；常用的频域闭环指标有谐振峰值Mp、谐振频率ωp和带宽频率ωb。其中，γc和Mp可表明系统的振荡程度，ωe、ωp和ωb可表明系统响应的快速性。
4．1．1 时域动态性能指标的定义
实际的系统，其输入信号和初始条件是各种各样的。为了便于研究，工程上常采用初始条件为零时系统对单位阶跃信号的响应来研究系统的过渡过程。因为阶跃信号便于测量，而且对系统来说，阶跃输入是最严峻的条件，所以，系统在阶跃信号作用下的性能指标若能满足要求，在其他形式输入信号作用下的动态性能，一般来说也能满足要求。图1．9－36为系统单位阶跃响应曲线，结合该图可给出时域动态性能指标定义：
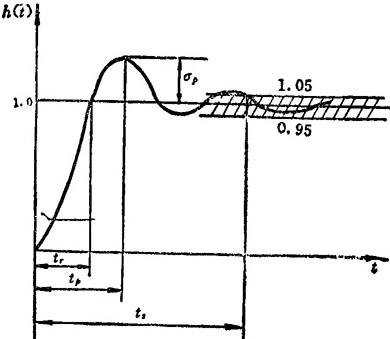
图1．9－36 系统单位阶跃响应曲线
①上升时间tr；响应曲线从稳态值的10%上升到90%，或从零上升到稳态值所需要的时间。
②峰值时间tp：响应曲线从零上升到第一个峰值所需要的时间。
③调节时间ts：响应曲线到达并保持在规定的误差范围内所需要的最小时间。调节时间也称为过渡过程时间。通常误差范围取稳态值的±5%或±2%。
④超调量σp：响应曲线的最大峰值与稳态值之差，称为超调量，常以百分比表示，即
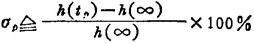
式中h(tp)、h(∞)分别为单位阶跃响应的最大峰值和稳态值。
4．1．2 动态性能指标的计算
一阶系统动态性能指标的计算公式：其数学模型为Φ(s)=1／(TS+1)。一阶系统的单位阶跃响应无振荡，误差范围取±5%、±2%时调节时间的计算公式分别为
ts(5%)=3T ts(2%)=4T(1．9－35、36)
式中 T为一阶系统的时间常数，T愈小系统响应愈快。
二阶系统性能指标的计算公式：其数学模型为Φ(s)=ω2／(sn2+2ζωns+ωn2)。式中ωn和ζ是二阶系统的特征参数；ωn为二阶系统无阻尼自然振荡频率；ζ为二阶系统的阻尼比。对应于系统不同的阻尼比，二阶系统的单位阶跃响应不同，参看表1．9－5．阻尼比值为0＜ζ＜1时的二阶系统称为欠阻尼二阶系统。工程上常把二阶系统设计成阻尼比为0．4＜ζ＜0．8的欠阻尼二阶系统(因为此时二阶系统综合动态性能较好)。欠阻尼二阶系统的时域动态性能指标计算公式如下：
表1．9－5 二阶系统的单位阶跃响应
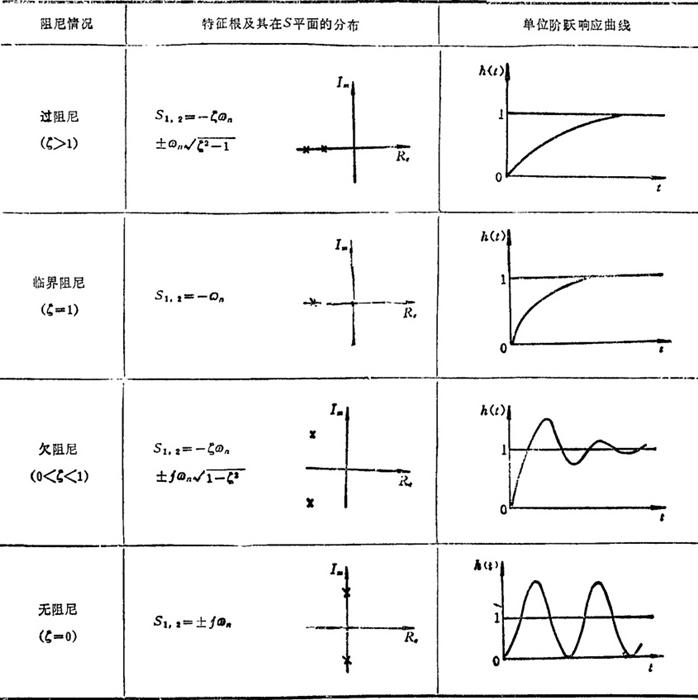
欠阻尼二阶系统频域开环指标ya和ωc可根据开环对数坐标图确定，频域闭环指标Mp、ωp和ωb可根据闭环幅频特性曲线确定，Mp、ωp也可利用下述公式计算：
计算高阶系统动态性能指标，其经验公式为：
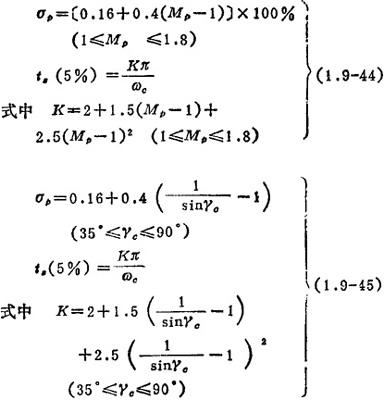
用数字计算机求高阶系统的数值解：设高阶系统的传递函数为
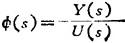
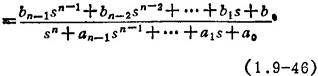
为便于计算机求解，将式(1．9－46)化成一阶微分方程组形式。引入中间变量X(s)，则上式可写成
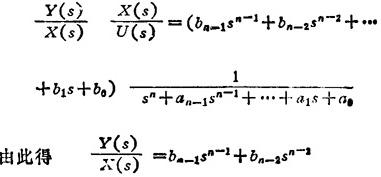
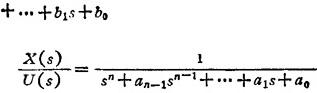
由以上两式可得如下两个微分方程和相应的初始条件：
y(t)=bn－1x(n－1)(t)+bn－2x(n－2)(t)+…+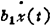
+b0x(t) (1．9－47)
x(n)(t)+an－1x(n－1)(t)+…+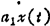
+a0x(t)=u(t) (1．9－48)
x(n)(0)=x(n－1)(0)=…=x(0)=x(0)=0
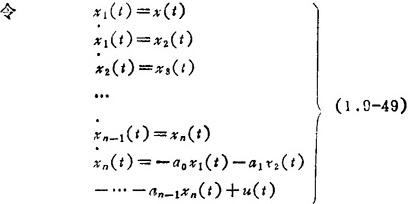
由式(1．9－47)和(1．9－49)得
y(t)=bn－1xn(t)+bn－2xn－1(t)+…+b1x2(t)+b0x1(t) (1．9－50)
方程(1．9－49)和(1．9－50)可以写成如下向量微分方程形式：
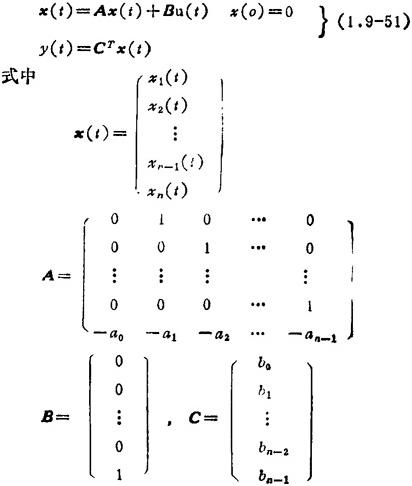
根据方程(1．9－51)，用扩展BASIC语言的矩阵语句，按照四阶龙格一库塔(Runge－Kutta)法编制求解y(t)的程序框图如图1．9－37所示［2］。通过计算机求出的不同时刻的y(t)，可画出高阶系统的单位阶跃响应曲线，据此可分析高阶系统的各项动态性能。
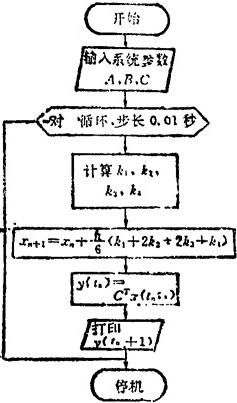
图1．9－37 求高阶系统数值解的程序框图