旋转的特征

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第117页（2945字）

经过旋转，图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度，任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等．

注意 1．旋转后的图形与原来图形完全重合，是全等形．

2．旋转中心在对应点连线的中垂线上．

例1 将下图中的甲图案变成乙图案，可以通过( )得到．

甲

乙

A．平移 B．旋转、平移

C．旋转 D．轴对称

答 B．

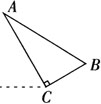
例2 如图所示，△ABO绕点O经过旋转得到△DEO，下列各角相等的是( )．

A．∠BOA与∠EOA

B．∠AOD与∠BOE

C．∠BOA与∠AOD

D．∠OED与∠A

答 B．

[解析] 旋转角相等．

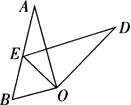
例3 如图，把菱形ABOC绕点O顺时针旋转得到菱形DFOE，则下列角中，不是旋转角的是( )．

A．∠BOF B．∠AOD

C．∠COE D．∠AOF

答 D．

[解析] 对应点与旋转中心连线所成的角是旋转角．

例4 同学们曾玩过万花筒，右图是万花筒中的一个图案，图中的所有小三角形都是大小相同的等边三角形，其中的菱形AEFG可以看成是把菱形ABCD以A为旋转中心( )．

A．顺时针旋转60°得到的

B．顺时针旋转120°得到的

C．逆时针旋转60°得到的

D．逆时针旋转120°得到的

答 D．

例5 如图所示，将左边的“心形”绕点O顺时针旋转95°得到右边的“心形”，如果∠BOC=75°，BO=2．8cm，则∠DOF=＿＿；∠COD=＿＿； DO=＿＿cm．

答 75°，20°，2．8．

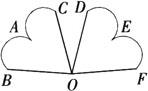
[解析] ∠BOC=∠DOF(对应角相等)，

∵∠COF=95°(旋转角)．∴∠COD=20°．

DO=BO(对应线段相等)．

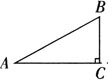
例6 直角三角形ABC中，∠C=90°，AC=6，BC=8，现将△ABC绕点B旋转90°，点A旋转到点D，则AD的长为( )．

A．20 B．10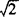

C．2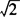0 D．10

答 B．

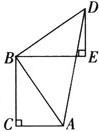
[解析] 如图所示，△DBE是△ABC绕B点旋转90°得到的三角形．

则△ABD为等腰直角三角形．(旋转角∠ABD=90°，对应线段相等AB=DB)

例7 如图，在等腰直角三角形ABC中，∠CAB=90°，P是△ABC内一点，且PA=1，PB=3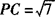．，求∠APC的度数．

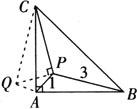
解 将△BAP绕点A逆时针旋转90°，使AB与AC重合，得到△CAQ，所以△CAQ≌△BAP，

∴AQ=AP=1，CQ=BP=3，∠CAQ=∠PAB．

∴∠PAQ=∠PAC+∠CAQ=∠PAC+∠PAB=90°：

在Rt△AQP中，PQ²=AQ²+AP²=1+1=2．

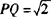∴，∴∠APQ=45°．

在△CPQ中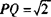，，CQ=3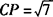，，∴CQ²=CP²+PQ²．

∴△CPQ是直角三角形，∠CPQ=90°．

∴∠APC=∠CPQ+∠APQ=90°+45°=135°．

例8 如图，正方形ABCD的边长为1，AB、AD上各有一点P、Q，如果△APQ的周长为2，求∠PCQ的度数．

解 将△DCQ绕点C逆时针旋转90°到△BCE，

则∠QCE=90°，CQ=CE，DQ=BE．

设AP=x，AQ=y，

则PB=1－x，QD=1－y=BE．

PE=PB+BE=1－x+1－y

=2－(x+y)=2－(AP+AQ)=PQ．

(△APQ周长为2)

∴△PCQ≌△PCE(SSS)，

∴∠PCQ=∠PCE=1/2∠QCE=45°．