高斯公式　通量与散度

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第198页（824字）

高斯(Guass)公式 设空间闭区域Ω是由分片光滑的闭曲面围成，函数P(x，y，z)，Q(x，y，z)，R(x，y，z)在Ω上具有一阶连续偏导数，则

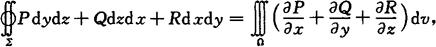
或

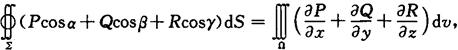
其中∑是Ω的整个边界曲面的外侧，cosα，cosβ，cosγ是∑与点(x，y，z)处法向量的方向余弦．

格林第一公式 设函数P(x，y，z)，Q(x，y，z)，R(x，y，z)在闭区域Ω上有一阶及二阶连续偏导数，则

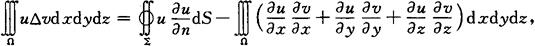
其中∑是Ω的边界曲面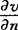，是函数v(x，y，z)沿∑的外向法线方向的方向导数，符号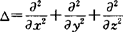称为拉普拉斯(Laplace)算子．

任意闭曲面的曲面积分为零的条件 设G是空间二维单连通域⁽¹⁾．P(x，y，z)，Q(x，y，z)，R(x，y，z)在G内有一阶连续偏导数，则

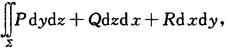
在G内与所取曲面∑无关而且取决于∑的边界(或G内任一闭曲面的上述曲面积分为零)的充分必要条件是G内恒有

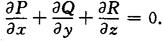
通量与散度

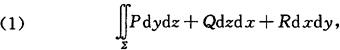
或

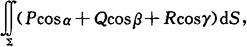
其中cosα，cosβ，cosγ是有向曲面∑的法向量的方向余弦．或

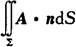
其中A=Pi+Qj+Rk，n=cosαi+cosβj+cosγk称为向量场A通过曲面∑的指定侧的通量(或流量)．

(2)向量场A的散度记为