二次型的矩阵表示，合同矩阵

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第332页（798字）

二次型

n元变量x₁，x₂，…，x_n的二次齐次多项式

…… (1)

当系数属于数域F时，称为数域F上的n元二次型．实数域上的二次型称为实二次型，简称二次型．

二次型的矩阵表示 令a_ij=a_ji，i＜j，则2a_ijx_ix_j=a_ijx_ix_j+a_jix_jx_i(i＞j)，则二次型(1)可表示成矩阵形式：

其中A是对称矩阵，A^T=A，称为二次型f的对应矩阵，且f与A一一对应．

线性变换 设两组变量，x₁，x₂，…，x_n；y₁，y₂，…，y_n，有关系

记成x=Cy，称为由x₁，x₂，…，x_n到y₁，y₂，…，y_n的一个线性变换，若其系数矩阵的行列式

则称线性变换是可逆线性变换(非退化线性变换)．

线性变换化二次型为新的二次型 二次型f(x₁，x₂，…，x_n)=x^TAx经可逆线性变换x=Cy化成二次型f=y^TC^TACy，它仍是二次型．

二次型的对应矩阵A，经过可逆线性变换x=Cy化成C^TAC．显然CTAC仍是对称矩阵．

合同矩阵 设A，B都是n阶矩阵，若存在可逆矩阵C，使得

C^TAC=B，

则称A合同于B，记作．

二次型的对应矩阵A，经可逆线性变换x=Cy得C^TAC(记为B=C^TAC)．则．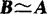

合同矩阵的性质