随机变量的函数的分布

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第389页（1215字）

这里所要解决的问题是：已知随机变量X的分布，随机变量Y是X的函数，Y=g(X)，g是连续函数，求Y的分布．

X为离散型随机变量

已知X的分布律P｛X=x_k｝=p_k，Y=g(x)，Y也是离散型随机变量．求Y的分布律．

所用方法为列举法．

(1)首先由X的取值经过Y=g(X)求出Y的取值．

(2)Y取值的概率，就是对应的X取值的概率，根据已知的X的分布律即可求出Y的分布律．

X为连续型随机变量

不能采用列举法．

在这里，已知什么?要求什么?要分析清楚．具体情况(关系)用下面方式(见图2．1)表示出来(→表示解题过程)．

图2．1

这里，F_X(x)，F_Y(y)分别表示X，Y的分布函数．f_X(x)，f_Y(y)分别表示X，Y的概率密度函数．

(1)已知F_X(x)，求F_Y(y)．利用定义，即

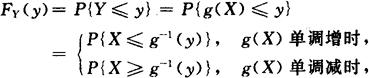
所以

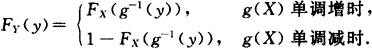
若欲求f_Y(y)，通过F_Y(y)对y求导，得到F′_Y(y)=f_Y(y)．

(2)已知f_X(x)，求．f_Y(y)．利用公式，有如下定理：

设X有概率密度函数f_X(x)，Y=g(X)，若y=g(x)在(a，b)上单调，可导，且g′(x)≠0，则Y有密度函数f_Y(y)，并且

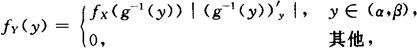
其中a=min［g(a)，g(b)］，β=max［g(a)，g(b)］．

若求F_Y(y)，可经过f_Y(y)对y积分得到

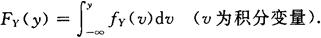
几个简单函数的分布

(1)若X～U(a，b)，Y=cX+d(c＞0)，则Y～U(ca+d，cb+d)．

(2)若X～N(μ，σ²)，Y=aX+b，则Y～N(aμ+b，a²σ²)．

(3)若X～E(λ)，Y=aX(a＞0)，则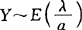．