资金时间因素的计算方法
出处:按学科分类—经济 南京大学出版社《新编经济师实用手册工业企业分册》第70页(1770字)
1.单利法
这是仅以本金为基数计算利息的方法。虽然考虑了资金的时间因素,但对以前已经产生的利息,并不转化为本金而累计计息。故对技术经济分析而言,不是完善的方法。其计算如式2-46所示。
F=P(1+ni) (2-46)
式中 F——本利和,或未来值;
P——本金,或现值;
i——利率;
n——利息周期(通常为年)数;
Pni——期末利息。
2.复利法
这是以本金与累计利息为基数的计息方法。即通常说的利上加利的计息法。此法能充分地反映资金的时间因素,是技术经济分析中常用的方法,也是我国现行信贷制度正在推行的方法。
复利法又分为普遍复利和连续复利两大类方法。每一类又依据支付利息的方式不同,有不同的计算公式。
(1)普通复利计算公式。是指以年复利计息,按年进行支付的复利计算公式。根据支付方式和等值换算时点的不同,普通复利公式又分为:一次支付未来值;一次支付现值;等额支付序列未来值;等额支付序列偿债基金;等额支付序列资金回收;等额支付序列现值;等差序列式或几何序列等不同的计息公式。这些公式及应用举例见表2-19。
表2-19 普通复利公式及应用举例
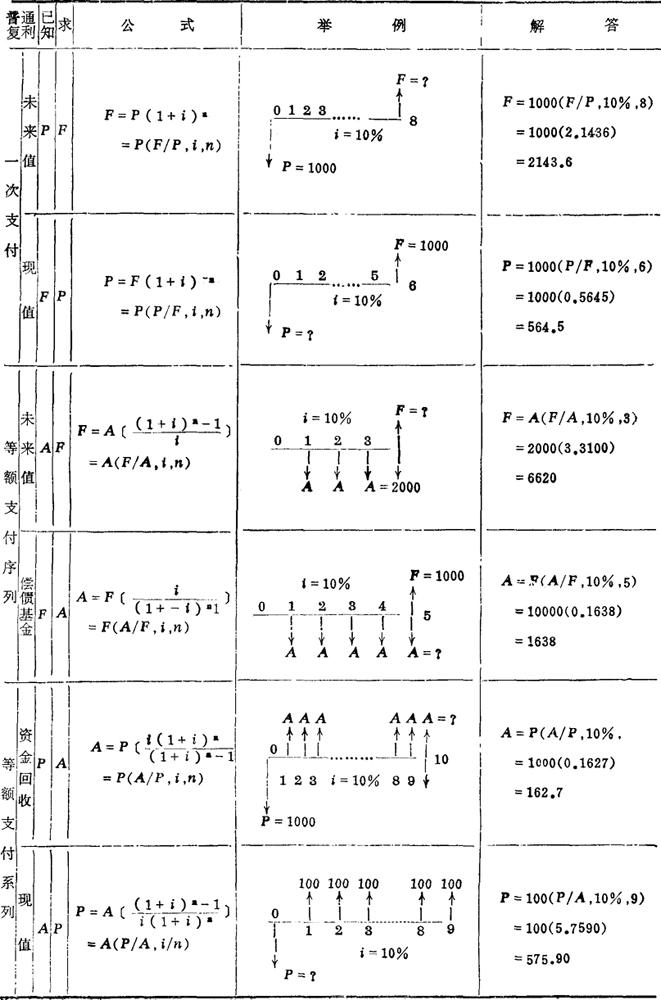

表2-19中的公式符号,除与单利法中的相同符号外,还有
A——等额年金序列;
G——等差变额;
j——逐年递增(减)的固定百分数。
表中的“举例”栏内,都是具体的现金流量时间图。图中:①座标单位为利息周期(通常为年);②每年发生的费用,均假定发生在每年的年末;③向上、箭头表示现金的收入(流入),向下的箭头表示现金的支出(流出)。
(2)连续复利计算公式。是指以小于一年为周期的复利计息,按半年或季或月或周或天进行支付的复利计算公式,这种计息方法更接近于实际,在理论上也较为完善。一些高级工程的技术经济分析,常采用连续复利法。此法又分为:连续复利计息、按年间断支付和连续复利计息、均匀连续支付等不同计算公式。其公式及应用举例见表2-20。
表2-20 连续复利(间断支付)公式及其应用举例


由于计息周期小于一年,则实际年利率要大于原规定的年利率。这样,原定的年利率称为名义利率(以r表示)。而实际利率(i)是按周期计息,并将利息的时间因素也考虑进去后的正年利率。
实际利率与名义利率的换算关系,见式2-47和式2-48。
表2-20中的符号,除与前面相同的外,还有:
e——为自然对数的底(=2.718);
r——名义利率(原定利率);
c——资金递增(减)率。

式2-47是普通复利的实际利率与名义利率的关系式。式中的m为实际计息周期次数。式2-48是连续复利的实际利率与名义利率的关系。