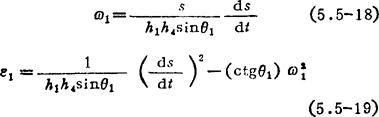空间RSCS四杆机构

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第1948页（956字）

在图5．5-15中，图a)所示为空间RSCS机构，图b)是用于飞机起落架上的示意图。当作为圆柱副的液压缸3通油时，与机轮相连的摇杆1即作摆动，从而实现起落架的收放。由图可以看出，RSCS机构中含两个局部自由度，柱塞2及液压缸3均可绕自身轴线转动，但并不影响摇杆1的运动。对RSCS机构进行运动分析，主要是求解杆2、3之间的相对伸缩量与摇杆1的转角关系。由于杆2、3为同一轴线，其间的相对伸缩量与B、C两球面副中心距3的变量相同。这样，在液压缸作为主动件时，s即可作为已知运动参数。

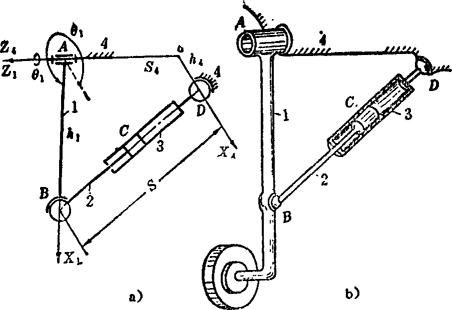
图5．5-15 空间RSCS机构

建立坐标系时，在机架4及摇杆1分别固结有坐标系a－X₄(Y₄)Z₄和A－X₁(Y₁)Z₁。Z₁轴选定和Z₄轴相重合，并沿着转动轴线。自球面副中心B、D所作Z₁(Z₄)轴的垂线，分别取为X₁轴和X₄轴。这样，机构的常量参数有：h₁=AB_，h₄=aD，s₄=aA；而主要运动参数除s外，还有摇杆1的转角θ₁。对着Z₄轴观察，绕Z₄轴，自X₄轴逆时针方向量至X₁轴时θ₁为正，反之为负。

由于图中坐标系a－X₄(Y₄)Z₄和A－X₁(Y₁)Z₁的关系与图5．5-11相同，故按式(5．5-1)和(5．5-2)得到球面副中心B点在坐标系a-X₄(Y₄)Z₄中的时变坐标为〔h₁cosθ₁，h₁sinθ₁，s₄〕T，球面副中心D点在a－X₄(Y₄)Z₄中的坐标为〔h₄，0，0〕^T。

采用拆杆法分析时，应将杆2、3一并拆离。这样，两球面副中心B、D两点间的距离应和s相等，因而可建立下列几何等同关系式：

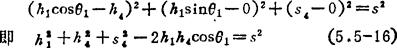
由此可得按已知s求解转角θ₁的公式为：

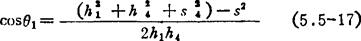
将式(5．5-16)对时间求导一次和二次，并注意到液压缸等速进油时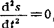，可得柱塞等速伸缩时从动摇杆的角速度和角加速度公式：