多变量函数微分法则
书籍:现代综合机械设计手册上
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第22页(825字)
7.5.1 偏导数
设z=f(x,y),则
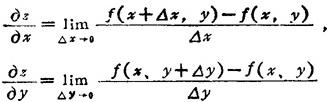
分别称为函数z=f(x,y),关于x、y的偏导数。其求法可按单变量函数微分法则求出,只须将其余变量看作常数。其定义可推广到多变量函数。
7.5.2 偏微分、可微函数、全微分
多变量函数对其中一个变量的偏微分为

若函数u=f(x,y)的全设变量可写为
△u=f(x+△x,y+△y)-f(x,y)=A△x+B△y+0Cρ)
式中A,B与△x,△y无关。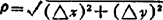 ,则称函数u=f(x、y)在点(x、y)可微分,且偏导数
,则称函数u=f(x、y)在点(x、y)可微分,且偏导数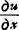 ,
,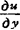 一定存在,而且
一定存在,而且
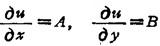
设变量的线性主部
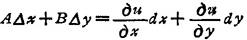
称为函数u=f(x,y)的全微分,记作
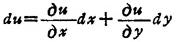
以上定义可以推广到u=f(x1,x2,x2,…xn)的一般形式。
7.5.3 复合函数微分法
设g=f(u,v,…,ω),而u,v,…,ω都是x,y,…,t的函数,则
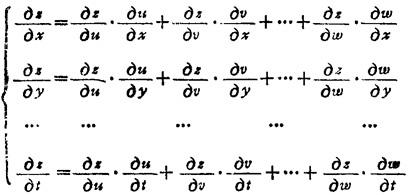
7.5.4 混合偏导数的性质
若混合偏导数连续,则与微分的顺序无关。例如:
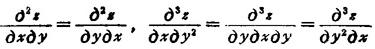
上一篇:简单函数的高阶导数
下一篇:现代综合机械设计手册上目录