达朗伯原理

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第84页（1089字）

3．4．1 惯性力和惯性力系的简化

质点在惯性空间以加速度a运动，则定义质点的惯性力为

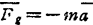(其中m为质点的质量) (1．2－48)

质点系中各质点的惯性力所组成的惯性力系可以向任一简化中心简化，得到一个等效的惯性力和惯性力偶。该惯性力的矢量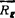等于原惯性力系的主矢，且可写为

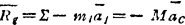
式中 M为质点系的总质量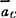；为质点系的质心加速度。该惯性力的大小和方向与简化中心无关。简化得到的惯性力偶，其矩等于原惯性力系对简化中心的主矩，该惯性力偶矩的大小和方向随简化中心选取的变化而将发生改变。

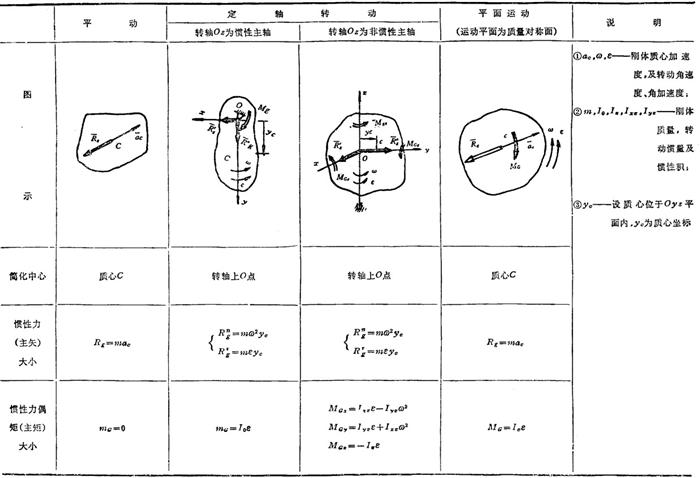
刚体作平动、定轴转动和平面运动时，其上各点惯性力系简化结果见表1．2－23。

表1．2－23 刚体惯性力系的简化结果

3．4．2 达朗伯原理

达朗伯原理：质点系(或单个质点)在运动过程的每一瞬时，各质点的惯性力与质点系的全部外力组成一个平衡力系。

动静法：就是根据达朗伯原理，按静力学的平衡方程式的形式来列写动力学方程的方法。

3．4．3 达朗伯原理应用举例

例1．2－3质量为2m的直角形匀质细曲杆CDE，固结于水平转轴AB(不计质量)上，且CD⊥AB，DE∥AB。尺寸如图1．2－16所示。若已知AB轴在力偶矩M的作用下，以匀角速度ω转动，且初瞬时曲杆CDE位于铅垂面内，求任意时刻轴承A、B两处的约束反力及力偶矩M的大小。

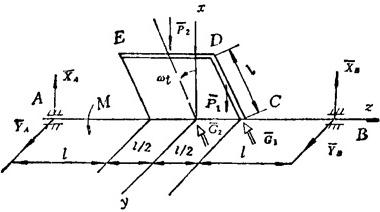
图1．2－16 曲杆转动的轴承反力

解：1．以曲杆和转轴为研究对象；2。对象所受已知力有转动力偶矩M、CD、DE的重力P₁=P₂=mg；约束反力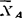、、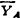、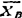；3．CD的惯性力G₁、DE的惯性力G2分别在它们的对称面内，且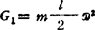，G₂=mlω²；4．建立图示坐标，有平衡方程：

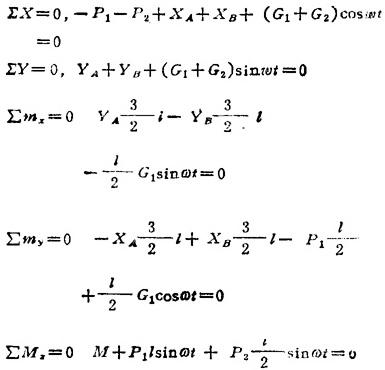
解方程并代入G₁、G₂之值便可得