频率特性

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第385页（2071字）

2．4．1 频率特性的定义

频率特性也称频率响应，是指线性定常连续系统(或元件)对正弦(或余弦)输入信号的稳态响应。频率特性是复函数，通常以G(jω)表示。线性元件(或系统)在正弦信号作用下，其稳态输出仍为同频率的正弦信号，只是幅值和相位会产生变化。稳态输出与输入的幅值之比，即频率特性的模丨G(jω)丨，称为幅频特性；稳态输出与输入的相位差，即频率特性的幅角arg〔G(jω)〕，称为相频特性。幅频特性与相频特性都是角频率ω的函数。

频率特性与传递函数一样，反映了系统的内在性质，只取决于系统本身的结构参数，与外作用无关。

2．4．2 频率特性的求取方法

频率特性可用如下三种方法得到：

①根据已知元件(或系统)的微分方程或传递函数，把输入以正弦函数代入，求其输出，取输出稳态分量和输入正弦函数的复数比即得。

例1．9－5 如图1．9－16所示机械系统，以力f(t)=Fsint为输入量，以位移x(t)为输出量，其微分方程为

其传递函数为

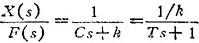
式中

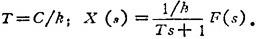
将F(s)=L〔Fsinωt〕=Fω／(s²+ω²)代入上式，并取拉氏反变换，可得x(t)为

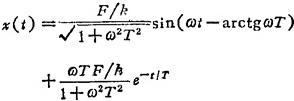
当t→∞时，上式右端第二项暂态分量衰减为零，则可得系统稳态分量为

该系统的幅频特性为

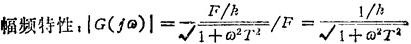
相频特性为：arg〔G(jω)〕=－arctgωT

频率特性为：

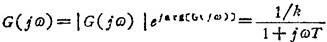
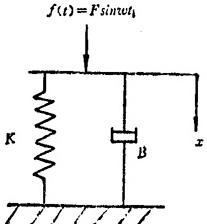
图1．9－16 机械系统

②根据传递函数求频率特性：将传递函数中的s用jω代替，就可得到系统或元件的频率特性，即

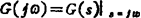
③通过实验求频率特性：对某些不能用分析法建立数学模型的系统，在系统的输入端加入一定幅值的正弦信号，稳定后系统的输出也是正弦函数，记录不同频率的输入，输出的幅值和相位，即可求得系统的频率特性。

2．4．3 频率特性的几何表示法

利用频率特性分析设计系统，一般不是利用其数学表达式，而是通过频率特性曲线图进行。常用的频率特性曲线图有如下三种：

①幅相频率特性图，也称极坐标图或奈魁斯特图。因为频率特性G(jω)是复数，对于给定的ω，可用复平面上相应的向量表示。现取ω为参变量，当ω从零到无穷大变化时，向量G(jω)的矢端在复平面上的运动轨迹，称为幅相频率特性曲线，该曲线连同坐标一起称为幅相图，如图1．9－17所示，规定幅相图的实轴正方向为相角的零度线，逆时针转过的角度为正角度，顺时针转过的角度为负角度。

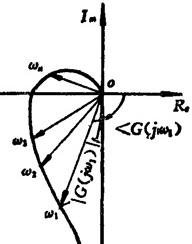
图1．9－17 幅相频率特性图

②对数坐标图，又称波德图，由对数幅频和对数相频两条特性曲线及其坐标组成，对数频率特性曲线的横坐标表示频率ω，并按对数分度，单位是rad／s，如图1．9－18所示。由图可知，ω的数值每变化10倍，在对数坐标上变化一个单位，该频带宽度称为十倍频程。对数幅频特性曲线的纵坐标表示系统输出与输入的幅值比丨G(jω)丨的对数值函数，均匀分度，常用单位是分贝，记作dB。对数幅频特性定义为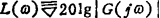：。对数相频特性的纵坐标表示相频特性的函数值，均匀分度，单位是度。

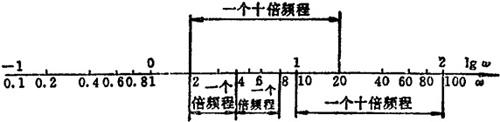
图1．9－18 对数坐标图的横坐标

③对数幅相频率特性图，对数幅相频率特性图也称尼柯尔斯图。其特点是横坐标和纵坐标都均匀分度，横坐标表示对数相频特性的相角，纵坐标表示对数幅频特性幅值的分贝数。图1．9－19所示是1／(1+jTω)在T取0．5时的对数幅相图。

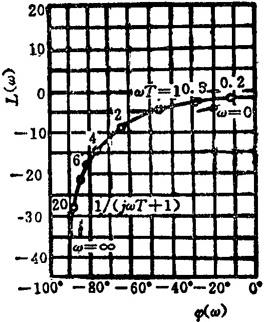
图1．9－19 对数幅相图