同位角、内错角、同旁内角

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第93页（892字）

如图所示，两条直线AB、CD被第三条直线EF所截，构成的8个角中：

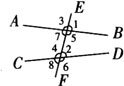
1．∠1与∠2这两个角分别在直线AB、CD的上方，EF的同侧，像这样的两个角叫做同位角．

2．∠5与∠4这两个角分别位于直线AB、CD的内侧，直线EF的两侧，像这样的两个角叫做内错角．

3．∠5与∠2这两个角在直线AB、CD的内侧，直线EF的同旁，像这样的两个角叫做同旁内角．

想一想：上图中还有哪几对同位角、内错角、同旁内角?

注意 1．形成这三类角的前提条件是：三线八角，即两条直线被第三条直线所截，构成8个角．

2．这三类角都是针对两个角而言的，而这两个角没有公共顶点，每个角都有一条边在同一直线(截线)上，另一边分别在另外两条直线(被截线)上．

例1 ∠1与∠4是＿＿角，∠1与∠3是＿＿角，∠3与∠5是＿＿，∠3与∠4是＿＿角．

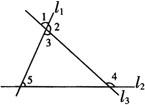
答 同位角、对顶角、同旁内角，内错角．

[解析] ∠1与∠4分别在直线l₁，l₂的上方，l₃的右侧，所以∠1与∠4是同位角．

∠1与∠3有公共顶点，且两边互为反向延长线，所以∠1与∠3是对顶角．

∠3与∠5分别在直线l₂，l₃的内侧，l₁的右侧，所以∠3与∠5是同旁内角．

∠3与∠4分别在直线l₁与l₂的内侧，l₃的两侧，所以∠3与∠4是内错角．