蒙特卡洛方法在预测中的运用

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第454页（2502字）

蒙特卡洛(Monte Carlo)方法是一种计算概率问题的方法。

是以概率与统计理论及方法为基础的。这种方法亦称为统计模拟方法、统计试验方法或随机抽样方法。

蒙特卡洛是地中海沿岸摩纳哥大公国中闻各世界的赌博城市。蒙特卡洛方法借用这一城市的名称，虽然是象征性的，但是在一定程度上表明了该方法的基本特征——概率问题。

从数理统计的角度来看，赌博是一种统计数学的实验。早期统计学家往往从赌博中胜败的可能性和概率来抽象出统计数学理论，并用以模拟某一事物活动过程统计其结果。

由于这种“模拟”方法来源于上述启示，故人称为“蒙特卡洛法”。

蒙特卡洛方法的基本思想，还可以追溯到两百多年前古典概率里着名的蒲丰氏问题。

18世纪法国科学家蒲丰(Buffon)用实验的方法求得下的近似值。即用向平面上等距离的平行线上投掷一枚针，而求其相交频数，作为针与平行线相交的概率的近似值，然后根据这一概率的准确结果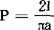，求出圆周率π的近似值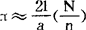：。其中2a是平行线的距离，21(1＜a)是针长，N是投针次数，n是相交次数。

要模拟真实情况，试验次数不能太少，要进行大量的试验，则又有很大的工作量，这就是在计算机没有出现前，这种方法本身没有多大发展和应用的原因，第二次世界大战结束后，计算机飞速发展，才使蒙特卡洛方法得到广泛应用。

蒙特卡洛方法作为一种计算方法，是由冯·诺伊曼(Von Nenmann)和乌拉姆(Ulam)在20世纪40年代中叶为研制核武器而首先提出的。当时在美国的洛斯－阿拉莫斯实验室(Los Alamos Lab)工作的物理学家需要计算中子在各个不同介质中游动的距离，中子的链式反应。他们利用数值的方法和技巧，在计算机上实现了第一个蒙特卡洛程序。跟踪大量中子，模拟每个中子游动的“生命”历史，然后作统计处理，使中子运动的统计规律性得以呈现。

近年来，随着模拟方法和计算机软件的发展，使模拟应用的范围迅速扩大。过去用数学方法来解决的问题，现在也开始为模拟技术所取代。

蒙特卡洛方法，可以用来模拟各种自然物理现象和物体的化学变化，并可用以模拟人类社会的经济活动过程等。运用蒙特卡洛方法求解某一问题可以归结为以下三个主要步骤：

(1)建立一个与问题相关的随机模型，确定描述研究对象行为的概率分布。在预测问题时，首先必须研究预测对象的基本行为，确定预测对象行为的概率分布。

(2)根据确定的概率分布进行随机抽样，又称为数字模拟。数字模拟可根据条件，用人工计算和计算机处理两种方式实现。对于大量的随机试验，只有用计算机处理，从已知的概率分布中抽样获得抽样值。

对于常见的概率分布，如均匀分布、正态分布、泊松分布等，都已编有现成的计算程序，可根据计算机的情况选用。

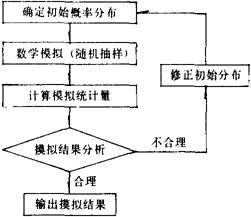
(3)根据随机模拟结果和基本预测模型，用数理统计和参数估计的方法，求取各模型参数，并进行预测或经济活动分析，给出预测结论，如果模拟结果与现实情况相差甚远，可以修正初始分布，再次进行模拟，以求得一个较为合理、较为符合客观现实的结果。

根据上述原理，蒙特卡洛模拟工作流程图如下：蒙特卡洛方法模拟技术为系统分析的预测人员提供了一个“实验室”，使人们可以在相当短的时间内，通过多种模拟实验，分析在一定的运行条件下，系统未来的状态和特征。

可以运用蒙特卡洛模拟技术，从以下几个方面分析和求解预测研究中的问题：

(1)在多目标预测和系统分析时，往往需要考虑到一组目标之间的相互影响和制约关系，以及各种随机因素的作用与干扰。

(2)预测中，经常遇到统计数据不足，即小样本的情况。这时，往往难以判断预测目标的总体分布如何。

在这种情况下，可以将蒙特卡洛模拟和统计检验方法结合起来，寻找预测目标的总体分布。首先，根据少量已知样本和主观经验，确定一个研究目标的初始分布；接着，运用蒙特卡洛模拟方法确定分布抽样；最后，用统计检验的方法判断已知统计数据和随机抽样数据是否来自同一“总体”，如果检验结果表明它们来自同一总体，这样我们就确定了研究目标的概率分布；若检验没有通过，则修正原假设，直至检验通过为止。找到了研究目标的概率分布，预测问题也就迎刃而解了。

(3)蒙特卡洛模拟技术还可以协助我们评价和选择参数估计方法。

蒙特卡洛模拟方法还可以用于以误差分析、预测区间估计等。

蒙特卡洛模拟是一种实验的方法，它不是按照传统的观念去求解模型，而是在假定的条件下，去运行这一模型，根据模型运行结果，进行预测分析和系统评价。

蒙特卡洛模拟的最大优点是其基本原理简单，易于领会，模拟得到的结果也易于管理人员理解。实际使用中，常常是先建立一个基本模型，如果模拟结果说明模型有效性不足，可以逐步扩充，把更详细更接近实际的细节纳入模型，以获得一个更精确的估计。其不足之处是由于只是根据精心设计的方案，通过模拟运行来分析可能出现的结果，而不是计算求解的，由于事实上不可能把所有的情况都考虑到，所以无法知道所选择的方案是否最为合理与有效。因此，它要求分析人员必须对所研究的对象具有相当的经验和洞察力，应使所选择的方案即使不是最切合实际的，也应该能较好地描述实际系统。另外，随着模型的复杂化，所需的费用也较高。