缓和曲线的特征及曲线方程

出处：按学科分类—工业技术 中国建材工业出版社《工程测量实用技术手册》第211页（1527字）

对于某一缓和曲线我们已知的数据有：

1)路线的转角△；

2)根据公路的等级和地形状况确定的圆曲线半径R；

3)缓和曲线的长度，可根据公路的等级和地形情况依表11－5查得；

4)交点JD的里程和曲线加桩的整桩间距。

表11－5 公路按等级与地形规定缓和曲线的长度

1．回旋曲线的特征和方程

缓和曲线是回旋曲线的一部分，回旋曲线的几何特征是：曲线上任何一点的曲率半径ρ与该点到曲线起点的长度l成反比。即：

式中 c——比例参数。我国公路设计规范规定c=0．035V³，V为设计的行车速度，以km／h计。

在缓和曲线的起点l=0，则ρ=∞。在缓和曲线的终点(与圆曲线衔接处)，缓和曲线的全长为l_h，缓和曲线的半径ρ等于圆曲线的半径，即：ρ=R。故上式可写成：

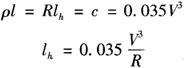
可知，设计的行车速度愈快，缓和曲线的长度应愈长；设计的圆曲线半径愈大，则缓和曲线的长度就可以相应缩短一些；而当圆曲线半径R达到一定的值以后，就可以不设置缓和曲线了。

2．缓和曲线的切线角公式

缓和曲线上任意一点P的切线与曲线起点ZH的切线所组成的夹角为β，β称为缓和曲线的切线角。缓和曲线切线角β实际上等于曲线起点ZH至曲线上任一点P之间的弧长l所对圆心角β。如图11－9所示。

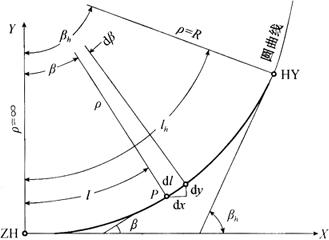
图11－9 缓和曲线切线角

在P点取一微分弧dl，它所对应的圆心角为dβ，则：

将公式ρl=Rl_h=c=0．035V³代入上式得

将上式积分：

当l=l_h时，缓和曲线全长l_h所对的切线角称为缓和曲线角，以β_h表示。

3．缓和曲线上任一点P坐标的计算

如图11－9所示，以缓和曲线起点ZH为原点，以过该点的切线为x轴，垂直于切线的方向为y轴。则任一点P的坐标可写为：

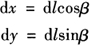
式中 dx、dy——纵横坐标微量。

将cosβ、sinβ按级数展开：

将上式代入dx、dy式中，再经积分整理后得：

上式称为缓和曲线的参数方程。

当l=l_h时，即得缓和曲线的终点坐标值：