正弦交流电的基本概念

出处：按学科分类—工业技术 江苏科学技术出版社《简明电工计算手册》第128页（4150字）

1．正弦交流电

大小和方向都随时间作周期性变化的电动势(电压或电流)称为交流电。交流电可分为正弦交流电和非正弦交流电两类，按正弦规律变化的交流电称为正弦交流电。不按正弦规律变化的交流电称为非正弦交流电。

根据电磁感应原理，交流发电机的线圈切割按正弦规律分布的磁场，则线圈中产生的感生电动势是按正弦规律变化的正弦交流电，其数学表达式为：

e=2NB_mlvsinα (2－83)

=E_msinα (2－84)

=E_msin(ωt+Φ) (2－85)

2．正弦交流电的相关名词

(1)瞬时值

任意时刻正弦交流电的数值称为瞬时值，其瞬时电动势、瞬时电压、瞬时电流分别用符号e、u、i表示。瞬时值有正、有负，也可能为零。

(2)最大值

最大的瞬时值称为最大值，其最大电动势、最大电压和最大电流分别用符号E_m、U_m和I_m表示。最大值虽然有正有负，但习惯上最大值都以绝对值表示。

(3)周期

交流电每重复一次所需的时间称为周期，用符号T表示，单位是秒(s)。常用的时间单位还有毫秒(ms)、微秒(μs)和毫微秒(ns)。换算关系如下：

1ms=10^－3s

1μs=10^－6s

1ns=10^－9s

(4)频率

交流电1秒钟内重复的次数称为频率，用符号f表示，单位是赫兹，用符号Hz表示，比赫兹大的常用单位是千赫(kHz)和兆赫(MHz)。换算关系如下：

1kH_z=10³H_z

1MH_z=10⁶H_z

根据周期和频率的定义可知，周期和频率互为倒数，即

(5)电角度

正弦交流电在变化过程中，决定其大小和方向的角度称为电角度，用符号α表示。正弦交流电每变化一周所经历的电角度为360°或2πrad(rad——弧度)。电角度并不是在任何情况下都等于线圈实际转过的机械角度的。只有在两个磁极的发电机中，电角度才等于机械角。在正弦交流电的数学表达式中出现的都是电角度，通常又称为相位或相角。

(6)角频率

正弦交流电每秒钟内变化的电角度叫角频率。角频率用符号ω表示，其数学表达式为：

式中 ω——角频率(弧度／秒，用符号rad／s表示)；

α——电角度(rad)；

t——时间(s)。

根据正弦交流电的频率与角频率的定义，可得ω与f的关系为：

根据角频率的定义，可知经过时间t变化的电角度α与角频率ω的关系为：

α=ωt (2－91)

(7)初相角及相位差

正弦交流电在开始计时起点(t=0)所对应的电角度称为初相角，也叫初相位或初相，用符号φ表示。正弦交流电在任何时刻的电角度α可表示为：

α=ωt+φ (2－92)

当t=0时，α=φ

两个同频率交流电的相位之差叫相位差，两个同频率交流电的相位差等于它们的初相位之差。

(8)正弦交流电的有效值

交流电的大小是不断变化的，难以取那个数值作为衡量交流电大小的标准，为方便计算和测量，通常根据交流电做功的多少来作为衡量交流电大小的标准。根据这个标准定义出来的量值就是交流电的有效值。让交流电和直流电分别通过阻值完全相同的电阻，如果在相同的时间内，这两种电流产生的热量相等，我们就把此直流电的数值定义为该交流电的有效值。换句话说，把热效应相等的直流电流(或电压，电动势)定义为交流电流(或电压、电动势)的有效值。交流电流、电压和电动势有效值的符号分别是I、U和E。

通过计算，正弦交流电的有效值和最大值之间有如下关系：

特别应指出的是，今后若无特殊说明，交流电的大小总是有效值。电气设备铭牌数据标注的交流电压，电流都是有效值。交流电表测出的数值都是有效值。显然，有效值不随时间变化。

3．正弦交流电的三要素

正弦交流电的最大值反映了正弦量的变化范围；角频率反映了正弦量的变化快慢；初相角反映了正弦量的起始状态，它们是表征正弦交流电的三个重要的物理量。知道了这三个量就可以唯一确定一个交流电，写出其瞬时值的表达式，因此常把最大值、角频率、初相角称为正弦交流电的三要素。

［例2－25］ 已知两正弦交流电的电动势分别是：。求：各电动势的最大值和有效值；频率、周期；相位、初相位、相位差。

［解］ 最大值

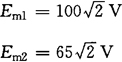
有效值

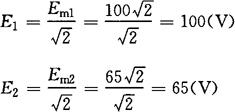
频率

周期

相位

α₁=(100πt+60°)

α₂=(100πt－30°)

初相位

φ₁=60°

φ₂=－30°

相位差

φ=φ₁－φ₂=60°－(－30°)=90°

4．正弦交流电的复数表示

正弦量可以用解析法(三角函数表示法)，波形图和相量法表示。相量用大写字母上打“·”表示，如。

如果把相量所在平面看成是一个复平面，那么表示正弦量的这个相量就唯一的对应一个复数。因此，正弦量也可以用复数来表示。其规则是：

①复数的模等于正弦量的最大值(有效值)；

②复数的辐角等于正弦量的初相角。

相量加、减，用复数的直角坐标形式，实部加或减，虚部加或减。相量乘、除，用复数的指数形式或极坐标形式，其相量的模相乘或相除，其辐角相加或相减。

［例2－26］ 已知正弦电动势，分别用复数的三角函数形式、直角坐标形式、指数形式和极坐标形式表示。

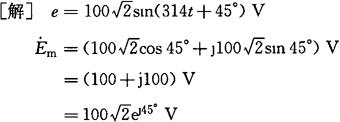
［例2－27］ 已知两个同频率的正弦电流分别是i₁=10sin(ωt+30°)A，i₂=8sin(ωt+60°)A，试用复数计算i=i₁+i₂。

根据可写出与它对应的正弦电流，即

i=17．4sin(ωt+43．3°)A

［例2－28］ 已知，求·，并列写U。

φ₁=135°(第二象限)

φ₂=－135°(第三象限)

［例2－29］ 已知，求。