数字电路
出处：按学科分类—工业技术 江苏科学技术出版社《简明电工计算手册》第297页（20245字）
1．逻辑关系
数字电路是指输出信号和输入信号之间存在一定逻辑关系的电路。
(1)与
当决定某件事情的各个条件都具备时，这件事情才发生，那么这件事情和各个条件的关系为与。
①表示与关系的电路。在图3－64中，只有当开关A和B都闭合时，灯F才亮，那么灯亮这件事情和开关A、B的关系为与。(开关之间串联即为与)
图3－64 逻辑与关系的实例
②逻辑表达式
F=A·B (3－265)
式中 F——输出量；
A、B——输入变量(A、B均有0或1两种状态)。
③与的计算口诀：有0出0；全1为1。
④逻辑符号，如图3－65所示。
图3－65 与门逻辑符号
⑤真值表，如表3－2所示。
表3－2 与门电路的真值表
(2)或
当决定某件事情的各个条件中，只要具备一个或几个时，这件事情都能发生，那么这件事和各个条件的关系为或。
①表示或关系的电路。在图3－66中，开关A闭合，或B闭合，或A和B都闭合，灯F都会亮，那么灯亮这件事情和开关A、B的关系为或。(开关之间并联即为或)。
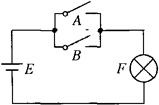
图3－66 逻辑或关系的实例
②逻辑表达式
F=A+B (3－266)
③或的计算口诀：有1出1；全0为0。
④逻辑符号，如图3－67所示。
图3－67 或门逻辑符号
⑤真值表，如图3－3所示。
表3－3 或门电路的真值表
(3)非
输出信号与输入信号保持相反的关系为非。
①表示非关系的电路。在图3－68中，E为电源电势，R为限流电阻，S为开关，F为灯。
图3－68 逻辑非关系的实例
设开关S闭合为1，断开为0；灯F亮为1，灯F暗为0。开关S断开为0时，电流经灯F形成回路，灯F亮为1。开关S闭合为1时，电流经开关S形成回路，灯F暗为0。灯F为输出，开关S为输入，两者信号始终保持相反的关系即为非。
②逻辑表达式
(3－267)
式中 S——输入量；
－——S上面的横线表示非。
③非的计算口诀：有0出1；有1出0。
④逻辑符号，如图3－69所示。
图3－69 非门逻辑符号
⑤真值表，如表3－4所示。
表3－4 非门电路的真值表
(4)与非
与和非的结合，即构成与非关系。
①逻辑表达式
②逻辑符号，如图3－70所示。
图3－70 与非门逻辑符号
③与非的计算口诀：有0出1；全1为0。
④真值表，如表3－5所示。
表3－5 与非门电路的真值表
(5)或非
或和非的结合，即构成或非关系。
①逻辑表达式
②逻辑符号，如图3－71所示。
图3－71 或非门逻辑符号
③或非的计算口诀：有1出0；全0为1。
④真值表，如表3－6所示。
表3－6 或非门电路的真值表
2．逻辑代数
逻辑代数是数字电路分析和设计的主要数学工具。
数字电路是反映输入与输出之间的逻辑关系。逻辑关系由逻辑函数表示。逻辑函数由逻辑变量A、B、C……和基本逻辑运算符号·(与)，+(或)，－(非)及括号，等号等构成的表达式来表示。如：
式中A、B、C称为原变量，
称为对应的反变量，F称为逻辑函数(
称为逻辑反函数)。
(1)逻辑加运算和法则
①逻辑加运算规则
0+0=0 (3－271)
0+1=1 (3－272)
1+0=1 (3－273)
1+1=1 (3－274)
②逻辑加运算法则
A+0=A (3－275)
A+1=1 (3－276)
A+A=A (3－277)
(2)逻辑乘运算和法则
①逻辑乘运算规则
0·0=0 (3－278)
0·1=0 (3－279)
1·0=0 (3－280)
1·1=1 (3－281)
②逻辑乘运算法则
A．0=0 (3－282)
A·1=A (3－283)
A·A=A (3－284)
注：对逻辑变量A、B进行逻辑乘运算，其结果用F表示，那么逻辑表达式为：F=A·B或者省略“·”，写成F=AB
(3)逻辑非运算和法则
①逻辑非运算规则
②逻辑非运算法则
(4)基本运算定律
①交换律
A+B=B+A (3－290)
A·B=B·A (3－291)
②结合律
(A+B)+C=A+(B+C) (3－292)
(A·B)·C=A·(B·C) (3－293)
③分配律
A+(B·C)=(A+B)·(A+C) (3－294)
A·(B+C)=A·B+A·C (3－295)
④吸收律
⑤冗余律
⑥狄·摩根定律
3．基本运算规则
(1)运算顺序
先算括号，再算非，然后算与，最后算或。
(2)代入规则
在逻辑等式中，如果在等式两边出现的某个变量，都用同一个逻辑式代替，则等式仍然成立，这就是代入规则。
例如，已知
，若A=D+E，则：
(3)反演规则
反演规则即狄·摩根定律。
(4)对偶规则
将逻辑式F中所有的乘，即“·”换成加，即“+”，所有的“+”换成“·”，“0”换成“1”，“1”换成“0”，变量保持不变，得到新逻辑式F′。F′称为F的对偶式。
例如，已知
，则其对偶式为：
4．逻辑函数的公式化简法
(1)并项化简法
利用公式
，把两个乘积项合并成一项，从而消去一个变量或表达式，剩下两个乘积项的公共因子。
［例3－24］ 试化简逻辑式
。
(2)配项化简法
利用公式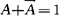
增加必要的乘积项，重配项，以便于消去其他项。
［例3－25］ 试化简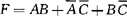
。
(3)吸收化简法
利用吸收律1，即A+AB=1，消去多余的项；利用吸收律2，即A+AB=A+B，消去多余的因子。
［例3－26］ 试化简逻辑式
5．逻辑函数的卡诺图化简法
(1)最小项
n个变量X1，X2，…，Xn的最小项是n个因子的乘积，每个变量都以它的原变量或反变量的形式在乘积项中出现，且仅出现一次。
举例来说，设A、B、C是3个逻辑变量，由这3个变量可以有8个乘积项，这些乘积项中各变量只出现一次，这8项即为最小项，每个最小项有3个因子。变量与最小项真值表如表3－7所示。
由表3－7可得到最小项的性质：
表3－7 变量与最小项真值表
①对于任意一个最小项，只有一组变量的取值使其值为1，而在变量取其他各组值时这个最小项的取值都是0。例如：
最小项为1的对应于变量组的取值是010，除此之外，其他变量组取值都使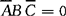
。
②对于变量的任一组取值，任意两个最小项之积为0。
③对于变量的一组取值，全部最小项之和为1。
用符号mi表示最小项。下标i是该最小项值为1时对应的变量组取值的十进制等效值，如最小项
记作m2，下标2对应最小项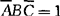
时变量组取值010，而010相当于十进制的2，因而下标i=2。由此可见表3－7中从左到右的8个最小项的表示符号分别为m0，m1，m2，…，m7。
(2)卡诺图
卡诺图是真值表的图形表示。图3－72分别表示了二变量、三变量、四变量和五变量的卡诺图。
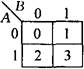
(a)二变量
(b)三变量
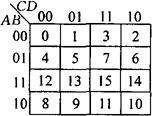
(c)四变量
(d)五变量
图3－72 卡诺图
有关卡诺图的说明：
①卡诺图中的每一个方格代表一个最小项，方格内的数字表示相应最小项的下标，最小项的逻辑取值填入相应方格。
②卡诺图方格外为输入变量及其相应逻辑取值，变量取值的排序不能改变。
③卡诺图中相邻的两个方格称为逻辑相邻项，相邻项中只有一个变量互为反变量，而其余变量完全相同。如图3－72(b)中4、5相邻方格，对应的最小项分别为
。除相邻的两个方格是相邻项外，卡诺图左右两侧、上下两侧相对的方格也是相邻项。如图3－72(c)中，方格4、6为相邻项，方格1、9也为相邻项。
(3)逻辑函数表达式画卡诺图
①逻辑函数最小项表达式画卡诺图。
若函数表达式是最小项表达式，例如，F(A，B，C，D)=∑m(0，1，3，5，10，11，12，15)，可根据图3－72(c)所示的四变量卡诺图的形式，将上述逻辑函数最小项表达式中的各项，在卡诺图对应方格内填入1，即在四变量卡诺图中，将与最小项m0，m1，m3，m5，m10，m11，m12，m15对应的格内填入1。四变量卡诺图中其余的方格内均填入0。最后得出如图3－73所示的F函数的卡诺图。
图3－73 卡诺图
②逻辑函数非最小项表达式，转换为最小项表达式画卡诺图。
若函数表达式是非最小项表达式，可先转换成最小项表达式，再画出其卡诺图。例如：G(A，B，C)=AB+BC+AC。有
在对应的卡诺图3－72(b)中最小项下标为3，5，6，7的方格内填入1，其余的方格内均填入0，得到如图3－74所示的卡诺图。
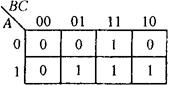
图3－74 卡诺图
③逻辑函数非最小项表达式直接画卡诺图。
非最小项表达式的函数表达式可直接画出卡诺图。例如，L(A，B，C)=A+BC。与项A对应卡诺图A=1一行下面四个方格，而与项BC对应卡诺图BC=11一列两个方格，在这些方格中填1，其余方格中填0，即可得到函数L的卡诺图，如图3－75所示。
图3－75 卡诺图
(4)卡诺图化简步骤
①画出逻辑函的卡诺图。方法如(3)所述。
②圈最小项。
圈最小项有圈1，圈0及利用约束项三种情况。一般采用圈1的方法，当逻辑函数的卡诺图中填1的方格较多，而填0的方格较少时，可通过圈0合并最小项进行化简，要比圈1合并最小项化简方便。圈0合并最小项，得到的是逻辑函数的非式，再通过取非法则，才能得到逻辑函数的表达式。
逻辑函数中不允许出现的输入变量组合所对应的最小项为约束项。约束项不作用于电路输入端，约束项使函数值取1或取0都不影响电路的输出。约束项可取1也可取0，利用约束项化简逻辑函数时，如圈1合并最小项时，可视为1，如圈0合并最小项可视为0。这样能方便地把逻辑函数化简为更简的形式(约束项用符号Φ表示)。
圈最小项的方法：
a．相邻的最小项可圈。
b．最大范围圈，但圈内方格数只能是2i(i=0，1，2，…，n)。圈内方格数越多，消去的变量越多，表达式就越简单。
c．最小项可重复使用，但是每画一个圈，至少有一个最小项未被圈过。
d．圈的个数应尽可能少。因为圈的个数越少，化简后的乘积项越少，得到的表达式越简单。
③合并最小项。
对各个圈过的最小项分别先进行列－列相加，行－行相加，然后列加－行加相与，最后将所有合并的最小项相加，从而得到简化的逻辑表达式。
［例3－27］ 试用卡诺图化简函数F(A，B，C，D)=∑m(0，1，2，4，5，6，8，9，12，13，14)。
［解］ ①画卡诺图。
将上述逻辑函数最小项表达式中的各项，在卡诺图对应方格内填入1，即在四变量卡诺图中，将最小项m0，m1，m2，m4，m5，m6，m8，m9，m12，m13，m14对应的格内填入1。其余的方格内均填入0。得如图3－76所示的F函数卡诺图。
图3－76
②圈最小项。
把相邻的8个方格m0、m1、m4、m5、m12、m13、m8、m9圈起来，把相邻的4个方格m0、m4、m2、m6圈起来，把相邻的4个方格m4、m12、m6、m14圈起来。
③合并最小项。
把所圈的8个方格进行，列－列相加，行－行相加，再列加－行加相与，得：
(注：相加时，互为反变量所对应的字母消去，互为同变量的字母保留)。
同理：
最后把合并后的乘积项相加，就可得到最简的逻辑表达式：
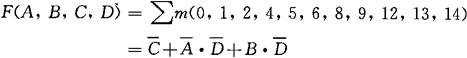
［例3－28］ 试用卡诺图化简函数F(A，B，C，D)=∑m(0～3，5～11，13～15)。
［解］ ①由函数F画出卡诺图，如图3－77(a)所示。
(a)卡诺图
(b)卡诺图圈
(c)卡诺图圈0
图3－77
②用圈1的方法化简，如图3－77(b)所示。得：
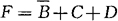
③用圈0的方法化简，如图3－77(c)所示。得：
两种化简方法的结果相同。
［例3－29］ 试用卡诺图化简逻辑函数F(A，B，C，D)=∑m(4，6，8，9，10，12，13，14)+∑d(0，2，5)。10，
该例为利用约束项化简逻辑函数。在逻辑函数表达式中约束项通常用∑d(－－－)表示，例如∑d(8，9，10)，说明最小项m8，m9，m10是约束项。有时也用逻辑表达表示函数中的约束项。例如
，表示
所包含的最小项为约束项。
［解］ ①由函数F画出卡诺图，如图3－78所示。
(a)
(b)
图3－78
②不考虑约束项，用卡诺图化简如图3－78(a)所示，其简化表达式为：
③考虑约束项，用卡诺图化简如图3－78(b)所示，其简化表达式为：
6．组合逻辑电路的分析
组合逻辑电路分析的主要任务是根据给出的逻辑图确定逻辑功能。其一般步骤如下：
①写出逻辑图输出端的逻辑表达式。
②化简和变换逻辑表达式。
③列出真值表。
④根据真值表和逻辑表达式对逻辑电路进行分析，最后确定电路的逻辑功能。
［例3－30］ 试分析图3－79所示逻辑电路的逻辑功能，要求写出输出表达式，列出真值表。
图3－79
［解］ ①从给出的逻辑图，由输入向输出，写出各级逻辑门的输出逻辑表达式：
②进行逻辑变换和化简
③列出真值表如表3－8所示。
表3－8 图3－79电路的真值表
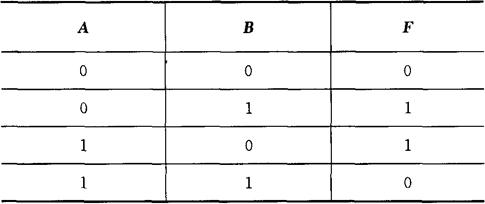
由表达式和真值表可知：图3－79逻辑图实现的逻辑功能是异或运算。
7．组合逻辑电路的设计
组合逻辑电路的设计，就是对给定的实际逻辑问题，构成逻辑电路的过程。通常组合逻辑电路的设计按下列四个步骤进行。
①列真值表。其方法是，根据给定的实际逻辑问题，确定哪些是输入量，哪些是输出量，以及它们之间的关系。然后对它们赋值，列出真值表。
②写表达式。其方法通常是由真值表写出最小项表达式。
③化简逻辑表达式。通常采用卡诺图化简法，输入变量多于四个时可用公式化简法。
④画出逻辑图。通常可根据简化表达式，用基本逻辑门组成逻辑电路。
［例3－31］ 设计一个三变量输入多数表决组合逻辑电路，即三个变量中有两个或三个同意时，表决通过。
［解］ ①设输入变量为A、B、C，输出变量为F。设A、B、C同意时为1，不同意时为0；输出F通过时为1，不通过为0。
然后，可根据该逻辑问题的要求，列出真值表，见表3－9。
表3－9 例3－31的真值表
②由真值表写出最小项表达式
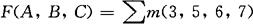
③用卡诺图化简该逻辑函数F，如图3－80所示。化简后得：
图3－80
F=AB+BC+AC
④按照表达式F=AB+BC+AC，可得逻辑图3－81所示。
图3－81 F=AB+BC+AC的逻辑图
［例3－32］ 作七段显示译码器。
荧光数码管是一种指形电子管，它由直热式阴极、网状栅极和七段互相独立的阳极组成。七段阳极的不同组合，可显示十进制数0～9十个数码，如图3－82所示。
［解］ ①以8421码为例，输入量为8421码A、B、C、D，输出量为数码管的七个显示段a、b、 c、d、e、f、g。按照图3－82所示的七段数字显示法，列出输出和输入之间关系的真值表，如表3－10所示。表中输出各显示段亮时用1表示，不亮时用0表示。
图3－82 七段数字显示方法
表3－10 七段显示译码器真值表
②由表3－10所示七段显示译码器真值表可画出7个显示段a、b、c、d、e、f、g的卡诺图，如图3－83所示。
图3－83 七段显示译码器卡诺图
③由于以上各卡诺图中为0的项少，故用圈0化简法，得各输出的表达式为：
以上为与或表达式，若用与非门组成译码器，表达式应变换为与非表达式：(用双非的方法并接合摩根定律即可变换)
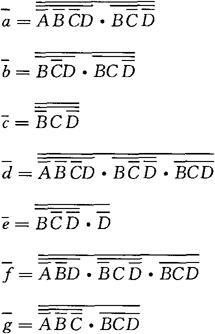
④根据以上与非表达式，画出七段显示译码器的逻辑图，如图3－84所示。
图3－84 七段显示译码器
8．触发器
触发器由逻辑门电路组成，它具有记忆和存贮功能，在某一时刻的输出不仅和当时的输入状态有关，而且还和在此之前的电路状态有关。即当输入信号消失后，触发器的状态被记忆，直到再输入信号后，它的状态才可能变化。
(1)基本RS触发器
基本RS触发器是最基础的触发器。
①电路的组成。基本RS触发器由两个与非门交叉耦合组成，如图3－85(a)所示。图中门D1和D2的输入、输出交叉连接，门D1、D2的另一个输入端RD、SD为触发器的输入端，门D1、D2的输出端Q、
为触发器的输出端。
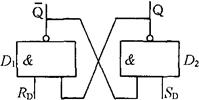
(a)逻辑图
(b)逻辑符号
图3－85 与非门组成的基本RS触发器
图3－85(b)为基本RS触发器的逻辑符号。输入端的小圆圈表示触发器由输入信号的低电平(用0表示)触发，或称低电平有效。触发器
的小圆圈表示触发器状态的非输出端，则Q为触发器的输出端。显然Q为高电平(用1表示)，则
为低电平，即Q＝1，
，触发器处于1态；若Q为低电平，则
为高电平，即Q＝1，
，触发器处于0态。
②逻辑功能。在触发器没有输入信号时，即RD=SD=1，触发器处于稳定状态，即保持原态；
当RD=1，SD=0时，触发器被置1，即被置位；
当RD=0，SD=1时，触发器被置0，即被复位；
当RD=SD=0时，触发器的状态不确定。触发器应避免RD=SD=0的输入状态。
③特性表。设定用Qn表示触发器的原状，即现态，用Qn+1表示加入触发信号后，触发器的新状态，即次态。根据对基本RS触发器工作原理的分析，将它的Qn+1、Qn、RD、SD之间的逻辑关系用表3－11所列的真值表来表示。该真值表反映了触发器的状态转换，通常称为特性表。
表3－11 基本RS触发器的特性表
在特性表中，第一，二两种状态属于RD=SD=0的情况，是不允许出现的，故对应的Qn+1用符号“Φ”表示不确定状态，Φ可以取0，也可以取1，是任意的。
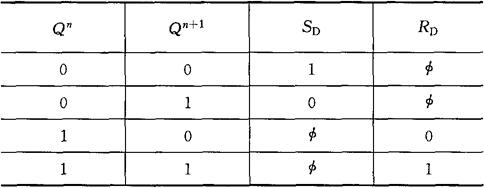
④驱动表。由触发器输出状态的转换来反映输入状态所对应的真值表为驱动表。
驱动表可由特性表转变而来。表3－11中的画线反映了由特性表转变为驱动表的对应关系。表3－12为基本RS触发器的驱动表。
表3－12 基本RS触发器的驱动表
⑤状态图。驱动表可用图形来表示。这种图形叫做触发器的状态图。图3－86为基本RS触发器的状态图。状态图比驱动表直观，图中圆圈内的数字表示触发器的状态，箭头线表示触发器状态转换方向，箭头线旁标注着进行该转换的输入值。
图3－86 基本RS触发器的状态图
⑥特性方程。表示触发器Qn+1和Qn、RD、SD之间关系的逻辑表达式称为特性方程。
由表3－11所示的基本RS触发器的特性表，可画出含有约束项的卡诺图，如图3－87所示。将该卡诺图化简后，可得基本RS触发器的特性方程为：
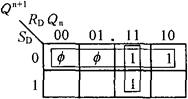
图3－87 基本RS触发器的卡诺图
式中 Qn——触发器的原状态，即现态；
Qn+1——加入触发信号后，触发器的新状态；即次态；
RD、SD——基本RS触发器的两个输入端。
式中约束条件RD+SD=1的含义是：RD、SD至少有一个为1，不允许同时为0。
(2)钟控RS触发器
基本RS触发器是由RD、SD输入端的触发脉冲直接控制的。如增设一个时钟控制输入端CP，只有CP输入端出现时钟脉冲时，触发器才能动作，其状态仍由R、S输入端的状态来决定，这类触发器就叫做钟控RS触发器，也叫做同步RS触发器。
如图3－88(a)所示，钟控RS触发器由与非门D1、D2组成的基本RS触发器和与非门D3、D4组成的控制门构成的。图中CP输入端是控制输入端，也称为时钟脉冲输入端。图3－88(b)为钟控RS触发器的逻辑符号。钟控RS触发器由输入信号的高电平(用1表示)触发，或称高电平有效。
(a)逻辑图
(b)逻辑符号
图3－88 钟控RS触发器
(3)主从RS触发器
为了解决触发器的输出受输入信号直接控制的问题，通常采用主从结构的触发器。
如图3－89(a)所示，主从RS触发器由两个钟控RS触发器组成，其中与非门D1、D2、D3、D4组成的钟控RS触发器称为从触发器，D5、D6、D7、D8组成的钟控RS触发器为主触发器。时钟脉冲CP除直接加到主触发器外，还经过非门D9反相后送到从触发器。电路中RD、SD为触发器的直接复位端和直接置位端。图3－89(b)为主从RS触发器的逻辑符号，CP端小圆圈表示下降沿触发(下降沿表示触发脉冲由高电平转变为低电平时)。
(a)逻辑图
(b)逻辑符号
图3－89 主从RS触发器
主从RS触发器的工作原理为：在CP=1期间，从触发器被封锁，主触发器被开启，R、S的状态决定主触发器的状态；在CP下降沿到来时，主触发器被封锁，从触发器被开启，从触发器的状态由主触发器的状态来决定。由于主触发器和从触发器总有一个开启，另一个被封锁，因此输入信号R、S的状态不直接影响主从触发器Q、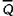
的状态。
(4)主从JK触发器
①电路的组成。图3－90(a)是主从JK触发器的逻辑图，电路中RD、SD为触发器的直接复位端和直接置位端。
(a)逻辑图
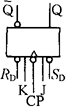
(b)逻辑符号
图3－90 主从JK触发器
与图3－89(a)所示的主从RS触发器相比较，将主从触发器的Q、
分别反馈到与非门D7、D8的输入端，并将S端作为J端，R端作为K端，这样就构成了主从JK触发器。
图3－90(b)为主从JK触发器的逻辑符号。
②逻辑功能。主从JK触发器具有时钟脉冲控制下的保持，置0、置1和计数翻转的功能，同时解决了输入端不能同时为1的约束条件，即J、K可以同时为高电平。主从JK触发器是一种功能比较齐全的触发器。
③特性表。表3－13为主从JK触发器的特性表，它反映了该触发器所具有的逻辑功能。
表3－13 JK触发器的特性表
④驱动表。主从JK触发器的驱动表可由其特性表转变而来。表3－14为主从JK触发器的驱动表。
表3－14 JK触发器的驱动表
⑤状态图。由主从JK触发器的驱动表，可作出主从JK触发器的状态图，如图3－91所示。
图3－91 JK触发器的状态图
⑥特性方程。由JK触发器的特性表，可画出其卡诺图，如图3－92所示。将该卡诺图化简后，可得主从JK触发器的特性方程为：
图3－92 JK触发器Qn+1的卡诺图
式中 Qn——触发器的原状，即现态；
Qn+1——加入触发信号后，触发器的新状态，即次态；
J、K——JK触发器的两个输入端；
－——符号上面的横线表示非。
(5)主从D触发器
①电路的组成。主从D触发器是在主从JK触发器的J、K输入端之间加一个非门构成的，如图3－93(a)所示。图3－93(b)为主从D触发器的逻辑符号。主从D触发器为时钟脉冲CP下降沿触发。
(a)逻辑图
(b)逻辑符号
图3－93 主从D触发器
②逻辑功能。主从D触发器的输出随输入D的状态而改变。
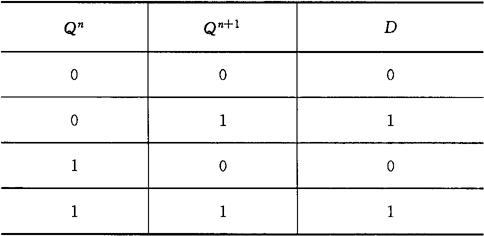
③特性表。表3－15为主从D触发器的特性表，它反映了该触发器所具有的逻辑功能。
表3－15 主从D触发器的特性表
④驱动表。主从D触发器的驱动表可由其特性表转变而来。表3－16为主从D触发器的驱动表。
表3－16 主从D触发器的驱动表
⑤状态图。由主从D触发器的驱动表，可作出主从D触发器的状态图，如图3－94所示。
图3－94 D触发器的状态图
⑥特性方程。由表3－15主从D触发器的特性表，可直接得到主从D触发器的特性方程为：
Qn+1=D (3－304)
式中 Qn+1——加入触发信号后，触发器的新状态，即次态；
D——主从D触发器的输入端。
(6)主从T触发器
①电路的组成。将主从JK触发器的J、K端相连接，并作为T输入端，就构成了主从T触发器，如图3－95(a)所示。图3－95(b)为主从T触发器的逻辑符号。主从T触发器为时钟脉冲CP下降沿触发。
(a)逻辑图
(b)逻辑符号
图3－95 主从T触发器
②逻辑功能。由主从JK触发器的逻辑功能可知，当T=0时，即J=K=0时，触发器保持原态，即现态。即Qn+1=Qn；当T=1时，即J=K=1时，触发器计数翻转，即
。
③特性表。根据主从T触发器的逻辑功能，可列出主从T触发器的特性表，如表3－17所示。
表3－17 T触发器的特性表
④驱动表。主从T触发器的驱动表，可由其特性表转变而来。表3－18为主从T触发器的驱动表。
表3－18 T触发器的驱动表
⑤状态图。由主从T触发器的驱动表，可作出主从T触发器的状态图，如图3－96所示。
图3－96 T触发器的状态图
⑥特性方程。由主从T触发器的特性表，可直接得到主从T触发器的特性方程为：
式中 Qn——触发器的原状态，即现态；
Qn+1——加入触发信号后，触发器的新状态，即次态；
T——主从T触发器的输入端；
－——符号上面的横线表示非。
(7)主从T1触发器
将主从T触发器的输入端T接高电平，即1，就构成了主从T1触发器，如图3－97所示。主从T1触发器为时钟脉冲CP下降沿触发。
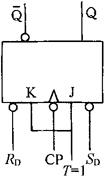
图3－97 主从T1触发器的逻辑图
在主从T触发器的特性方程中，令T=1，得：
因此主从T1触发器的特性方程为：
9．时序逻辑电路的分析
时序逻辑电路和组合逻辑电路不同，时序逻辑电路任何时刻的输出信号不仅取决于该时刻的输入信号，而且还取决于电路原来的状态。
时序逻辑电路的分析，就是根据给定的时序逻辑电路图，通过分析，求出它的输出F的变化规律以及电路状态Q的转换规律，进而说明该时序逻辑电路的逻辑功能和工作特性。其分析步骤如下：
①根据给定的时序电路图写出下列各逻辑方程式：
a．各触发器的时钟脉冲CP的逻辑表达式。
b．时序电路的输出方程。
c．各触发器的驱动方程。
②将驱动方程代入相应触发器的特性方程，求得各触发器的次态方程，也就是时序逻辑电路的状态方程。
③根据状态方程和输出方程，列出该时序电路的状态表，画出状态图或时序图。
④用文字描述给定时序逻辑电路的逻辑功能。
需要说明的是，上述步骤不是必须执行的固定程序，实际应用中可根据具体情况加以取舍。
［例3－33］ 对图3－98所示的同步时序逻辑电路进行分析。
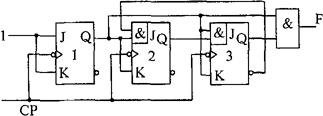
图3－98
［解］ ①根据图3－98所示的时序逻辑电路，列写各逻辑方程式。(由于该电路为同步时序逻辑电路，各触发器的时钟脉冲CP均相同，故各触发器的CP逻辑表达式可以不写)。
输出方程
驱动方程
②将驱动方程代入相应触发器的特性方程
KQn(该电路所用的触发器为JK触发器)，求出各触发器的次态方程。
③列状态表。先填入输入和现态的所有组合状态(本例中无输入变量，故状态表中此项，只有现态
)，然后根据输出方程及现态方程，逐行填入当前输出F的相应值，以及次态
)的相应值。由此可列出例3－33的状态表，如表3－19所示。
表3－19 例8－33状态表
④状态图。根据状态表可画出这个电路的状态图，如图3－99所示。由状态图可见，000、001、010、011、100、101这6个状态形成了闭合回路，在电路正常工作时，电路状态总是按照回路中的箭头方向循环变化，因此这6个状态构成了有效序列，称它们为有效状态，其余的2个状态称为无效状态。
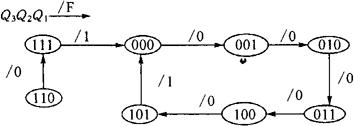
图3－99
⑤时序图(即波形图)。若设电路的初始状态为
=000，根据状态表和状态图，可画出在一系列CP脉冲作用下的时序图，如图3－100所示。
图3－100
⑥逻辑功能分析。由状态图可看出，此电路在正常工作时，是一个六进制加法计数器，在时钟脉冲作用下，
的数值从000到 101递增，每经过6个时钟脉冲作用后，电路的状态循环一次，当3个触发器的输出状态为101，电路输出F=1，否则，F=0。此外，由状态图还可看出，电路在正常工作时是无法达到无效状态的，若此电路由于某种原因，如噪声信号或接通电源迫使电路进入无效状态时，在CP脉冲作用后，电路能自动回到有效序列，电路的这种能力称为自启动能力。通常，希望时序电路具有自启动能力。