出现新设备条件下的更新决策方法

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第731页（4285字）

前面讨论的是设备在使用期内不发生技术上过时和陈旧，没有更好的新型设备出现的情况。在技术不断进步的条件下，由于第Ⅱ种无形磨损的作用，很可能在设备运行成本尚未升高到该用原型设备替代之前，就已出现工作效率更高和经济效果更好的设备。这时，就要比较在继续使用旧设备和购置新设备这两种方案中，哪一种方案在经济上更为有利?

在有新型设备出现的情况下，常用的设备更新决策方法有：年费用比较法和更新收益率法。

1．年费用比较法

年费用比较法是通过分别计算原有旧设备和备选新设备对应于各自的经济寿命期内的年均总费用，并进行比较，如果使用新型设备的年均总费用小于继续使用旧设备的年均总费用时，则应当立即进行更新，反之，则应继续使用旧设备。

(1)旧设备年总费用的计算

这里讲的旧设备的经济寿命已不是原来意义上的经济寿命了，它是指从决策时刻算起，直到应该报废时为止的期限，在这段期限自然也存在年均总费用的问题。但值得注意的是，在决策年份，旧设备已运行多年，每年实际运行的费用，会超过该设备经济寿命期内的年平均总费用，即它已处于“U”型曲线谷底以后的时期，在大多数情况下，旧设备的年均总费用将随着设备使用年限的延长而逐年增加。所以，在进行设备更新决策时，旧设备的经济寿命通常只有一年。这里，同新设备经济寿命期的年均总费用相比的旧设备的费用，实际上就用下一年的总费用即可。旧设备年总费用的计算公式为：

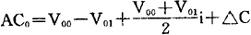
式中 AC₀——旧设备下一年运行的总费用；

V₀₀——旧设备在决策时可出售的价值；

V₀₁——旧设备一年后可出售的价值；

△C——旧设备继续使用一年在运行费用方面的损失(即使用新设备相对使用旧设备

的运行成本的节约额和销售收入的增加额)；

i——年利率；

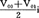——因继续使用旧设备而占用资金的利息损失，资金占用额取旧设备现在可售价值和一年后可售价值的平均值。

(2)新设备年均总费用的计算

用于同旧设备年总费用比较的新设备年均总费用。主要包括以下几个方面：

第一，运行劣化损失，新设备随着使用时间的延长，同样也存在设备劣化的问题，劣化程度也将随着使用年数的增多而增加。具体的劣化值取决于设备的性质和使用条件。为了简化计算，假定劣化值逐年按同等数额增加，如果设备使用年限为T，T年间劣化值的平均值为：

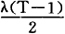
式中λ——设备年劣化值增量。

新设备的λ值往往是难以预先确定的。一般可根据旧设备的耐用年数和相应的劣化程度来估算新设备的年劣化值增量。

第二，设备价值损耗。新设备在使用过程中，其价值会逐渐损耗，表现为设备残值逐年减少。假定设备残值每年以同等的数额递减，则T年内每年的设备价值损耗为：

式中：K_n——新设备的原始价值；

V_L——新设备使用T年后的残值。

第三，利息损失。新设备在使用期内平均资金占用额为：

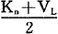
故因使用新设备而占用资金的利息损失为：

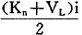
总计以上三项费用，则得新设备年均总费用：

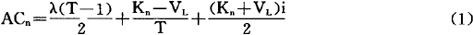
对上式进行微分，并令

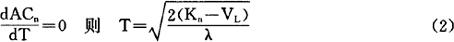
式中：T——新设备的经济寿命。

将(2)式代入(1)式得按经济寿命计算的新设备年均总费用：

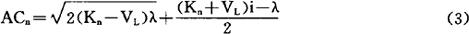
若残值V_L=0，则可简化为：

当年劣化值增量λ不易求得时，可根据经验决定新设备的合理使用年数T，然后再求年劣化值增量λ。这时将(2)式经整理后再代入(1)式，则新设备的年均总费用：

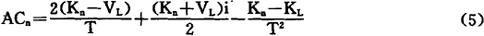
2．更新收益率法

更新收益率法是通过计算更新与不更新两种方案的差额投资的收益率判别是否应该进行设备更新的。由于这种方法给出的是一个收益率指标，可以用于同其它各种投资方案进行比较以寻求最有利的方案，因此它有更广泛的适用性。计算更新收益率的基本公式如下：

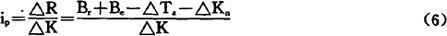
式中i_p——更新收益率；

△K——更新方案相对于不更新方案的增量投资；

△R——更新方案相对于不更新方案的增量收益；

B_r——运行性收益，即使用新设备相对于使用旧设备在第一年收益增加额和运行费用节约额的合计；

B_e——运行外收益，即因设备更新而在第一年避免的资产价值损失；

△T_a——使用新设备相对于使用旧设备在第一年缴纳税金的增加额；

△K_n——新设备使用一年的价值损耗。

其中 △K=K_n－(V_L0+K_r0) (7) B_e=V_L0－V_L1+△K_r0 (8)

△T_a=(B_r-D)r_T (9)

△K_n=△K-K₁ (10)

以上四式中

K_n——新设备的购置安装投资；

V_L0——旧设备在更换年份的残值；

K_r0——继续使用旧设备当年必须追加的投资；

V_L1——旧设备继续使用一年后的残值；

△K_r0——继续使用旧设备所需追加投资在第一年的分摊额；

D——新旧设备年折旧额的差额；

r_T——所得税税率；

K₁——新设备第一年末的保留价值。

将式(10)代入式(6)可得

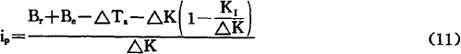
式(11)中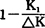，称为新设备价值损耗系数，表示新设备在第一年的价值损耗占更新投资额的比例。计算更新收益率的关键在于求出这一系数。

计算新设备价值损耗系数，首先应明确新设备第一年末保留价值K₁的经济涵义。

K₁既不是新设备第一年末的可售价值，也不是新设备原值扣除第一年折旧的净值，而是设备更新方案从第二年起直到新设备经济寿命结束时为止的全部净收益和新设备期末残值以第一年年末为基准年的现值合计。

设新设备的经济寿命期为n年，在新设备经济寿命期内各年，因设备更新而获得的税后净收益为B_t(t=1，2，…，n)，新设备在寿命期末可回收的残值为V_nL，则设备更新净投资△K的内部收益率i^*可由下式求得

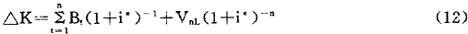
如果我们把△K看成是新设备的初始价值(确切地说是“设备更新方案”的初始价值)，则新设备的初始价值可理解为在新设备经济寿命期内因设备更新而获得的全部税后净收益和新设备期末残值按i^*折算的现值合计。新设备在使用过程中会不断发生价值损耗，假定新设备第一年价值损耗恰恰等于第一年的税后收益，则新设备第一年末的保留价值应等于从第二年起直到新设备经济寿命结束为止各年税后净收益和新设备期末残值以第一年末为基准年按i^*折算的现值合计，即

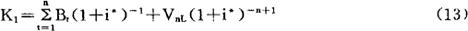
要计算K₁，首先需知道在新设备寿命期内各年由设备更新带来的净收益，而这些数据是不可能在进行更新决策时预先确知的。在更新收益率法中，我们作了更新收益逐年递减的假定。

由于存在着设备的有形磨损与无形磨损，设备更新所带来的净收益一般是逐年递减的。据有关研究，收益递减模式可以简化归纳为三种。第一种称为普通标准型。更新收益随新设备使用年限的延长呈线性递减，到新设备经济寿命结束时净收益为零。第二种和第三种为非标准型，更新收益随使用年限延长呈非线性递减，到新设备经济寿命结束时净收益为零。