抽样调查的一般知识
出处：按学科分类—农业科学 中国农业出版社《植物保护统计手册》第47页（20209字）
一、概念与应用范围
(一)抽样调查的几个基本概念
1．抽样调查 是一种非全面调查。所谓抽样调查，是指按随机的原则，在研究对象的全部单位或全及总体中抽取一定数量的单位进行观察，并将观察得出的抽样指标，用以推断全及总体指标的一种组织形式。由于这种形式是在概率论与数理统计学的基础上建立起来的，既包含搜集统计资料的方法，又包含对全部研究对象的数量特征进行估计推断的方法，达到对总体的认识。因此，抽样调查在统计调查和统计分析中，是一种很有用处的调查方法。
2．全及总体和抽样总体 从调查统计的范围看，全及总体简称总体，是指将所要研究的调查单位的全体。总体单位数通常用符号N表示。抽样总体简称样本，是指从总体中被抽取出来的，用抽样调查方法所要直接观察的全部单位。样本的单位数通常用符号n表示。样本是抽样调查的特有概念。从理论上讲，样本总是小于总体的，是总体的缩影。因此，它是推断总体的依据。然而，总体单位N很多，有时多得无法计算；而抽样单位n则远比N为小，可小到N的几十、几百乃至几千、几万分之一。抽取样本的多少，主要取决于研究对象的观察性质和研究的具体任务。从总体中抽取的单位可以构成一个抽样总体，也可以构成一系列的抽样总体；而且每一个抽样总体可以计算相应的综合指标。
3．总体指标与样本指标 总体指标是指以总体各单位标志值计算的综合指标。样本指标是指以样本总体各单位标志值计算的综合指标。总体指标是由总体全部标志总量所决定的，也是唯一确定的量，总体的总平均数就是一例。样本指标则不同，它是随着样本单位的不同而参加样本指标计算的，标志总量亦就不同，它仍然是一个随机变量，样本平均数就是一例。在数理统计中，样本指标称为统计量，它是总体随机变量的函数。从理论上说，样本统计量可以有多种多样的，但实际上常用的只有抽样平均数和抽样成数。
总体平均数，是指总体的平均数，一般用符号
表示。
总体成数简称成数，是指总体的成数，通常用符号P表示。
样本成数简称频率，是指样本的成数，通常用符号p表示。
(二)抽样调查的应用范围 抽样调查的应用范围与抽样调查的目的及调查对象性状有着密切联系。应用范围主要有如下几点。
1．对不可以用或难于应用全面调查的客观事物进行调查研究，以取得总体数量的特征 如对玉米螟、甘蔗螟虫等钻蛀性害虫密度的调查，不可能将所调查的玉米、甘蔗都砍下剥查，而只能采用抽样调查的组织形式。又如对某乡进行水稻三化螟的发生量及发生程度的定量和定性调查，同样地不可能逐田块甚至逐株检查，而且也没有这个必要。只能采用抽样调查，按随机原则抽取一定数量的样点村、样点田调查，获得有关指标，以满足人们调查统计的需要。关于定量和定性的计算方法，待第七章详述。
2．对全面调查或普查资料进行修正和补充 在全面调查或普查过程中，往往由于面广、工作量大而造成人为误差。例如人口普查的净差率(遗漏率－重复率)。为了减少误差，提高可靠程度或验证调查结果、积累有关统计指标，在开展全面调查或普查之后而进行的抽样调查。如某地区植保站组织一次全地区性植物检疫对象——柑桔黄龙病的普查。为了验证、修正和补充普查资料，确定发生范围、发生危害程度等指标。普查结束，首先对各县普查资料进行粗略地比较，结合该病传入本地区各县的历史资料以及所影响普查质量的有关情况进行分类，按随机原则，应用类型抽样形式确定样点县、样点乡，进行抽样调查，然后计算净差率，即可获得上述有关统计指标，完成对普查资料的验证、修正和补充的任务。
二、抽样误差
(一)抽样误差的概念 抽样误差是指抽样指标与总体指标之间所产生差数的简称。误差是不可避免的。因为样本指标是根据抽样单位的标志值计算出来的，而总体中的其他没有被抽到的单位标志值则没有被计算在内，而且通常以抽样指标来代替总体指标。
(二)抽样误差的计算公式
1．抽样误差的计算原理 前面已介绍了抽样误差是抽样指标与总体指标之间的差数。这些差数一般又是以抽样平均数或成数来推算总体平均数或成数的。所以，抽样误差主要是抽样平均数与总体平均数之间的差数(
)或抽样成数与总体成数之间的差数(p－P)。这些差数的产生是由于样本从总体的抽样过程中会产生一系列的抽样指标以及一系列的抽样误差。根据数理统计的证明，总体平均数(或成数)与从总体中抽出一系列样本的抽样平均数(或成数)的总平均数是相等的。因此，计算一系列抽样平均数(
)对总体平均数(
)的平均差数，与计算一系列抽样平均数(
)对一系列抽样平均数的总平均数(
)的平均差数是一致的。然而，计算抽样误差，是指计算一系列抽样误差的平均数，即计算一系列抽样平均数(或成数)的标准差。那么，可通过计算标准差的方法来计算抽样误差(实际上是指抽样平均数的平均误差，不同)。其计算公式为
式中 
——抽样平均数的平均误差；
μp——抽样成数的平均误差；
——抽样平均数的标准差；
——样本平均数；
——样本平均数的总平均数；
N——总体单位数；
n——样本单位数。
例如：总体为1、2、3、4、5个数字组成，按随机不重复抽样方式抽取三个数字组成一系列样本。样本平均数就有10个｜
｜。现将各样本平均数和抽样误差列出如表3－1。
表3－1
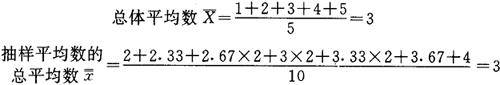
用上式计算结果：
所以，此例抽样平均数的平均误差(或抽样平均数的标准差)为0．58。
2．影响抽样误差大小的主要因素 数理统计的标准差，是反映平均数代表程度的尺度；用抽样方法来推算总体所产生的平均误差，是反映总体指标代表程度的一种尺度。因此，抽样误差愈小，样本的代表性愈高。为了减少一系列抽样误差，提高样本代表性，从抽样方案设计到抽取样本的过程中，必须注意如下影响抽样误差大小的几个主要决定性因素：(1)抽样单位的多少。样本单位数抽取愈多，则抽样误差愈小；反之，样本单位数抽取愈少，则抽样误差愈大。(2)总体标志变动程度的大小。一个样本单位标志是全及总体各单位标志中之一。总体各单位标志的变动程度愈小，抽样误差就愈小；反之，总体各单位标志的变动程度愈大，抽样误差就愈大。由此可见，抽样误差的大小，与抽取单位数多少成反比，与总体各单位变动程度的大小成正比。(3)抽样调查的组织形式不同。不同的抽样形式所具有可靠程度的高低也是不一样的。一般来说，应用类型抽样和机械抽样要比纯随机抽样、典型抽样更能保证抽取的单位在总体中均匀地分布，从而降低了误差程度。此外，重复抽样和不重复抽样对抽样误差也有不同程度的影响。从理论上来说，不重复抽样比重复抽样所产生的误差要小些，但在样本足够多的情况下，误差是很小的，所以在实际工作中却采用重复抽样条件下的抽样误差计算公式。
3．抽样误差的计算 对于抽样误差的计算，应该遵照上述计算公式进行，但事实上在全及总体单位很多，甚至无法计算时，不可能抽取所有的样本单位，加上全及总体指标也无从知道。根据数理统计关于标准差的理论，在重复抽样的条件下，采用纯随机抽样的抽样误差，即抽样平均数的标准差等于全及总体的标准差(δ)除以抽样单位数(n)的平方根。所以，抽样平均误差(
)计算公式如下：
这由于
，
的结果。
从上述公式可明显地看出，抽样误差与总体的标准差是成正比的，与抽样单位数n的平方根成反比例。
从总体中抽取样本有重复抽样和不重复抽样之分。它们的共同点为每一单位都有被抽中的机会。不同之处：被抽选的任一单位，前者仍再参加下一次抽选，使各单位被抽中的机会先后是相等的；后者则不再参加，被抽中的机会在不断地变动；从总体个数变动来看，前者单位数始终如一，后者则在每一次被抽取多少单位，总体单位数就相应地减少多少。上面所介绍的是重复抽样误差的计算公式，至于不重复抽样误差计算公式，只不过在重复抽样误差计算公式根号内乘以一个系数(1－n／N)，或在重复抽样误差计算公式乘以一个系数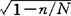
而已。其公式如下：
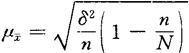
现用这个公式计算前述5个数字(1，2，3，4，5)的总体。抽取3个数字为样本的平均抽样误差为：
首先计算总体标准差：
然后代入上式计算，得：
例如：在室内饲养苎麻夜蛾三龄幼虫5000头，以观测其历期，另在田间饲养5000头作对照，待蜕皮成四龄幼虫后，各随机选取100头计算其历期。室内饲养平均历期为2．9天，标准差为0．8天；田间对照的平均历期为2．4天，标准差为0．9天。求室内和田间苎麻夜蛾幼虫历期。
已知室内饲养的幼虫：n=100，N=5000，
，δ=0．8
代入上述公式，得：
计算结果，室内5000头三龄幼虫的平均历期为2．9±0．079天之间，即2．82－2．979天之间。
已知田间对照的幼虫：n=100，N=5000，
，δ=0．9
代入不重复抽样误差计算公式，得；
计算结果，田间对照的5000头幼虫的平均历期为2．4±0．089天之间，即2．311－2．489天之间。由此可见，在田间饲养的苎麻夜蛾三龄幼虫历期，绝大部分都比室内的短，符合一般规律，资料是可靠的。
至于抽样成数的平均误差计算方法，只有掌握了上述抽样误差的计算方法后，就较容易、简便地掌握和应用。理论证明，总体成数的标准差平方为P(1－P)，只有将P(1－P)代替上述公式中的δ2才可以得到抽样成数的平均误差。计算公式为：
例如，从一批棉花种子中，以不同方位随机抽取200g，检验带有红铃虫的种子(不合格)占10g，即成数P=0．05，若以概率要求0．6827，即±0．6827，±1δ内，试求这批种子不能调入的成数。
已知 n=200，P=0．05，1－P=0．95。
代入上述公式，得：
这批种子不能调入的成数为0．05±0．015，即在0．035－0．065之间，或3．5%－6．5%之间。这结论的准确度概率为0．6827，即68．27%。
又如大面积防治吹绵蚧施药后检查死亡率，检查虫数500头，其中死虫占312头，即占62．40%，求与抽样误差联系的死亡率。
已知 n=500，P=0．624，1－P=0．376。
代入上述公式，得：
介壳虫的死亡率为62．40%±2．2%，即62．2%－64．6%。
从上述重复与不重复的两个抽样误差计算公式相比较，相差一个系数(1－n／N)，这个数值永远小于1。可见在同等条件下，不重复抽样的平均误差，永远小于重复抽样的平均误差，如果抽样单位很小，而总体单位很多时，则(1－n／N)接近1，这对于平均误差影响不大。因此，在实践工作中，为减少计算上的麻烦，按不重复抽样方法抽样的往往采用重复抽样误差的计算公式。
特别指出的是，抽样调查是在不需要或不可能对总体进行全面调查的情况下采用的，因而，计算抽样误差公式中的总体平均数标准差δ和总体成数标准差
的数值，在计算抽样误差时，实际上是未知数，所以一般都用样本的标准差来代替计算。因而，纯随机抽样误差的计算公式中的δ是用样本平均数的标准差代替；P是用样本成数代替。而且在统计实际工作中也只能抽取一个或少数若干个样本进行调查。
三、样本单位数目的确定
(一)确定抽样数目的重要性 对于病虫草鼠抽样调查方案的设计，必须遵循抽样原理，还要认真考虑经济效益、精确度、总体编号的难度、田间实际抽样工作中解决具体问题的难易程度等因素。归根结底，就在于如何合理确定抽样数目问题。若抽样单位过多，虽然提高了样本对总体的代表性，但浪费人力、物力、费用和时间，还会影响抽样调查的实施，从而失去抽样调查应有的优越性；反之，抽样数目愈少，节约了人力、物力和费用，但又会使抽样误差增大。数理统计已证明，只有当抽样总体的单位数足够大时，抽样平均数的分布都接近于以全及总体平均数为中心的正态分布，从而保证了样本对总体的代表性，所以合理确定抽样数目极为重要。
(二)影响抽样数目的因素
1．总体标准差的大小 总体标准差是指总体中各单位之间标志变异程度。要求的标准差或方差数值大时，抽样数目就多一些；反之，标准差或方差数值小时，抽样数目可以少一些。
2．允许误差数值的大小 我们可以从允许误差计算公式
中明显地看出允许误差的大小与样本数m成反比。所以，允许误差大可以少抽些样本单位，允许误差小则要多抽一些样本单位。
3．要求把握程度的高低 把握程度就是概率，它是根据抽样方案的要求而定。要求把握程度高的，则t值就小，样本则要多抽一些；反之，要求把握程度低的，即t值就大，样本可少抽一些。
4．选择抽样形式或方法的不同 一般来讲，采用类型抽样，或有关标志排队的机械抽样等方式时，要比纯随机抽样需要的样本少。重复抽样时，抽取的样本多些；不重复抽样时，抽取的样本就少些。
(三)抽样数目的计算
1．根据样本平均数确定抽样数目的计算
在重复条件下的计算公式：
上式等号两边乘方得
上式移项即得如上计算公式
式中
为允许抽样平均误差。
在不重复抽样条件下的计算公式：
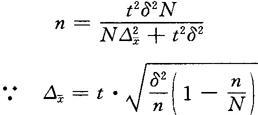
上式等号两边乘方得：
上式经通分、多次移项即得如上计算公式。
例如：对某县96000亩水稻田稻飞虱的密度进行抽样调查。现已知全县加权平均百丛禾有稻飞虱的标准差为65头，要求把握程度为F(t)为0．9545，允许误差
为20头，求需要抽取多少亩(块)水稻田作样本?
已知N=96000亩，给定的可靠程度F=0．9545，t=2［查F(t)表得］，△
=20，δ=65头。
将上述已知数据代入计算公式，得：
在重复抽样条件下：
在不重复抽样条件下：
若每块田的面积为1亩，那么在重复抽样条件和不重复抽样条件下，按要求均需抽取43块水稻田作样本。
2．根据抽样成数确定抽样数目的计算
在重复抽样条件下的计算公式：
上式等号两边乘方得：
将上式移项即得如上计算公式。
上式中△p为允许抽样成数误差。
在不重复抽样条件下计算公式：
上式等号两边乘方得：
上式等号两边除以t2后又移项即得如上计算公式。
例如：对出口柑桔10万公斤进行柑桔溃疡病检疫，按收货人的定货合同要求，果实不带柑桔溃疡病病斑率为96%，允许误差为3%，概率保证程度达95%。问需要抽查多少公斤柑桔?
已知：N=100000kg，P=96%，△p=3%，F(t)=95，t=1．96［查F(t)表得］。
将上述的数据代入计算公式，得：
在重复抽样条件下：
计算结果，在重复抽样和不重复抽样的条件下，均需抽取柑桔164kg。
前面已讲过，在组织抽样的实际工作中，由于n／N的比值很小，不重复抽样与重复抽样相差很小；同时，不重复抽样确定抽样数目的公式很复杂。因此，以不重复抽样的也按重复抽样的公式计算抽样数目。
一般来说，测定平均数所需抽取的单位数(nx)和测定成数(np)所需抽取的单位数是不相同的，即nx≠np。但在实际工作中，为了保证抽样调查的准确程度，通常采用其中较大的n值作为统计的单位数。从上述两个例子的计算结果看，重复抽样与不重复抽样的抽样数是不相等的，但相差极微，如柑桔的抽样仅相差0．27。这是由于总体量多和P值大的缘故。
以上几例的计算结果说明，它包含了小数在内的近似值的整数，并非按通常四舍五入的处理原则。
四、抽样调查的组织形式及其误差
(一)抽样调查的组织形式 抽样调查可以根据调查研究的目的、调查对象的性质、抽样误差的允许范围以及人力、物力、经费的节约程度等情况，针对性地采用不同的组织形式。抽样组织形式可分为随机抽样、机械抽样和典型抽样三大类。其中随机抽样可分为纯随机抽样、类型抽样、两级或多级抽样、双重抽样。
1．纯随机抽样 又称简单随机抽样。所谓纯随机抽样，是指从总体全部单位中，按随机原则，抽取调查单位组成样本的一种组织形式。在实际抽样工作中，可有不同的抽样方法。通常采用的一是抽签法，二是运用《随机数表》法。
抽签法的步骤是：先将全部总体单位逐个加以编号，再将号码制成标签，然后将其混合均匀，随着用手摸取或用摇号机摇出任意号码。被摸出或摇出的号码上所属的单位就是样本单位。
运用《随机数表》，该表是事先已编好的，见表3－2。
表3－2 随机数表(部分)
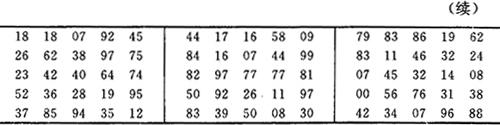
其步骤是：如对含有60个单位的总体抽取6个样本。首先编号为0－59；其次，假定随机以《随机数表》的第二行第四列开始为起点取号，按从上到下的顺序对照抽号，直到抽够6个样本数为止。按以上所给的条件查表3－2，结果表中第二行第四列的数为67，此号不在0－59的编号之内，则不取。继续向下查找取号，此号为27，它是在0－59的编号之内，此号可取。这样继续依次序查找取得了35、53、34、32、19共6个样本号，达到了目的。值得注意的是，在抽取样本过程中，若属重复抽样条件的，遇上重复的号码，可视为有效数字；若不属重复抽样条件的，可视为无效数字，即相同编号的仅能抽1次。
纯随机抽样方式，在理论上最符合随机原则，而且较单纯，是抽样调查的基本方式。但在实际工作中，总体单位多时，难于实施。另外，在总体各单位之间的某个数量标志的差异程度比较大时，以此方式调查及推断总体的精确度就受到影响。如植物保护专业统计，对一个村，甚至一个乡、一个县的水稻病虫密度、发生(为害)程度的定量定性调查工作中，总体单位(田块、品种)数多，若要逐块又分品种编号很困难，也不可能办到。所以，不宜直接应用，而是与其它方式配合应用。但对于范围小，如一片、一块田而且地势、肥力、灌溉水平直至作物品种等基本一致的情况下，也就是说总体单位不多，而且分布较均匀的，可直接应用之。
2．类型抽样 又称分层抽样或分类抽样。它是指先将总体各单位的主要标志分组(区层)，然后在各组内按随机原则，抽取一定单位构成样本。类型抽样是把分组法和抽样原理结合起来，从而提高了可靠程度。
类型抽样的优点：
一是提高样本的代表性，特别是比例抽样，可使样本单位构成接近于总体的构成。因为在抽样前已经掌握了并利用总体各抽样单位的变异性，划分为若干同质类型及其各占的比例。如某县按抽样设计的要求，计算确定全县抽样调查水稻纹枯病的田块总数为300块，然后按地理位置(北、中、南部)或按发生程度(轻、中、重)的面积比例分别计算各调查区域的田块数，并按各调查区的类型田(早、中、迟熟)的面积比例分别计算各类型的田块数。如表3－3。
表3－3 ××县按面积及类型田的比例确定抽样田块数表
二是可以缩小抽样误差，因为经分类后，各类型组中各单位都有被选中的机会，属于抽样形式，仍存在抽样误差。由于各类型组都会被选中，属于全面调查性质，因此，类型间则不存在抽样误差。
三是对病虫发生及为害程度的调查，这种方法特别适宜。因为病虫在田间发生为害作物的自然分布是非随机性，也因作物的类型田及长势不同，导致了病虫密度有稀疏和稠密现象。若调查前对于上述总体性质有所知道，分别在不同病虫密度或按各类型田的比例进行抽样，这样所得的结果一定比纯随机抽样为精确。
3．机械抽样 又称等距抽样和顺序抽样。它是指将总体各单位以某一标志按其自然顺序进行编号排列，分为相等单位数量的组，组数等于拟从总体抽出的单位数目，随机地从第一组抽取第一个样本，然后依固定顺序组和等距间隔从第二组内抽取第二样本，这样，直至抽足所需样本数。
机械抽样的优点：
一是方法简单，田间工作不易发生差错。
二是事先不必作许多随机抽样步骤，从而节省抽样准备工作时间等。
三是样本在总体中分布均匀，缩小各单位之间的差异程度。
但是，值得注意的是，当抽取调查单位时，要尽量避免抽样间隔与现象本身周期性的变化相重合而引起的误差。如田块内或田块之间的肥瘦以及品种等的变异所引起的病虫分布不均等变异现象。如不注意，所抽出的样本对总体的代表性就差。另外，机械抽样所获得的数据不可能得出一个正确的抽样误差估计，因而也无法对总体平均数或成数计算其可靠的置信范围。针对这个问题，可采取与其他抽样形式相配合，利用其能计算抽样误差的特点等，克服了上述不足之处。为此，提出如下两种配合作法：(1)机械抽样与整群抽样配合。假若将机械抽样看作一个单位群，那么，不可能计算抽样误差，但可以从总体的自然编号的第一组内随机抽出n个顺序样本，从而获得几个单位群，这样就可以计算出机械抽样的抽样误差了。例如，在400行的玉米田调查玉米大斑病，按抽样成数10%抽取样本。机械抽样是在第一组10个单位内随机抽取1个，然后间隔每10个单位抽取1个，这样得出40个单位可看作1个单位群，但不可能估计抽样误差。通过与整群抽样配合，其抽样误差的计算就得到了解决。其做法是：抽取的样本数不变，仍为40个单位。但已由原来1个群变为8个群，又以每群包括5个单位来代替上述1个群包括40个单位了。抽样步骤为：将总体内号码(0－399)分为5个组，每组80个单位。从第一组80个单位中，按随机数字抽出8个随机数字组成第一组，再逐群每间距80个单位抽1个单位。这样依顺序抽取第二、三、四、五组，即可随机地获得8个群的40个样本号码。将其号码列于表3－4。(2)机械抽样与两级抽样配合。两级抽取的样本，其抽样误差仅仅根据从初级单位间的变异即可获得正确估计了，而不必考虑次级单位之间的变异；同样地，只要用随机方法确定初级单位的分配就可以了。例如，调查某地区棉田的棉盲蝽为害程度，将这一地区所有棉田的田块当作初级单位，再以每块田内分出纵横各5株共25株的面积为次级单位。采用机械抽样与两级抽样配合的方法，通过随机抽样抽取n1块棉田，然后在抽选棉田内，每块田用机械抽样如5点取样式或对角线取样方式抽出n2个次级单位。这样的配合既可得出有代表性的平均数的无偏估计，而且有准确的抽样误差估计。这说明了混合抽样类型的方法是有特殊作用的。
表3－4 采用机械抽样得出8个群的样本
然而，机械抽样可分为随机的机械抽样和非随机的机械抽样。上述几种属于随机的机械抽样。但目前病虫害抽样调查或试验小区观察抽样常用的是机械抽样法，如棋盘式、对角线式、五点式、平行线式、分行式和Z形式等取样法，所获得的数据虽然可得出有代表性的平均数和成数，但仍不能获得抽样误差，因此仅能称为非随机的机械抽样法。只有象上述那样将机械抽样与其它抽样方法配合作用，机械抽样才是合理的和被经常使用的。
此外，在组织机械抽样时，可根据研究的具体任务和被调查现象的特点，把总体各单位按某一标志排队分为按有关标志排队和按无关标志排队。
所谓按无关标志排队，是指总体排队所用的标志与调查研究的目的和总体单位标志值的大小无关或不起主要影响作用的。时间、地区或人为的顺序等就是如此。例如，对一外轮的进口小麦抽查植物检疫对象，在通过传送带将船仓里的小麦输出船外时，按每5分钟抽取样本观察1次，及时掌握检疫对象有否等情况。
所谓按有关标志排队，即是采用与调查目的和总体标志值大小有关的标志排队。如水稻三化螟越冬虫口密度抽样调查，选择该虫的虫源田(板田、犁冬田、绿肥田)，每类型田3块，每块虫源田以单对角线五点取样式，按随机原则，以等距抽选样点，且每点查6平方米田中稻根的三化螟活幼虫数，以推断各类型田每亩虫口密度。
4．整群抽样 又称为集团抽样，是指每次抽取到的单位不是一个而是一群(批)，被抽取的所有单位均进行调查。就是说，对总体各群体进行的调查属抽样调查方式，而对每个群体内进行的又是全面调查。如调查早、中、迟播晚稻秧田的稻瘿蚊为害率，以每块田随机五点取样，每点查1平方米(群)所有秧苗的为害苗数及未受害苗数。
整群抽样的优点：组织方式比较简单，被抽中的单位比较集中，调查工作亦比较简单。
整群抽样的不足之处，由于被抽取的整群数目受到限制，加上被抽中的单位比较集中，便会影响样本单位在总体中的均匀分布，从而降低样本的代表性。在样本单位数目等条件相同的情况下，一般整群抽样比其他抽样方式的误差大。只有当各群体代表性较强的情况下，抽样误差才会小。所以减少抽样群内单位数，多抽一些抽样群，其抽样误差才能得到有效地控制和缩小。
整群抽样与类型抽样相比较，两者在抽样之前均需要将所有总体单位划分为若干部分或群体。由于两者划分标志的性质不同，抽取样本和计算抽样误差的方法也不同。类型抽样以有关标志划分组，而整群抽样则以无关标志划分组；类型抽样是在每一类型组中分别随机抽取部分总体单位作样本，即对类型组间是全面调查，对类型组内是抽样调查，而整群抽样则从总体各部分群体中随机抽取一部分群体样本，即群体间是抽样调查，对群体内是全面调查，整群抽样的抽样误差计算方法是与类型抽样的正好相反。前者是用组间方差，代替简单随机误差计算公式中的总方差来计算；后者则用组内平均方差。
5．两级抽样或多级抽样 两级抽样，是指将对调查对象采用的抽样方法分为两级或两阶段(次)进行：一是从总体中随机抽取抽样单位，称为初级单位；二是仍从每个被抽出的初级单位中再随机抽取的抽样单位，称为次级单位。三级或多级抽样，是指从选出的每一个次级单位再随机抽取第三级(次)抽样单位。例如对某果园的苹果树进行抽样，即为第一阶段，对苹果的抽样则为第二阶段，这就是两级抽样，均为随机抽样单位。若对抽出的苹果(二级抽样)再进行随机抽取样本的，即是三级或多级抽样。
两级或多级抽样的特点：
一是有些调查研究不可能对一些初级单位内的次级单位进行全面调查。例如，对苹果树的果实病虫为害率调查。
二是有利于解决全部编号问题，因而节约人力和时间。例如，上述苹果园的果实受病虫害为害率调查，易于编出全果园的果树编号，而且随机抽样也容易；但难于对每一树上的苹果进行全部编号以及随机抽取单位。
三是此法较之纯随机抽样获得更精确的结果。倘能和其他抽样方法结合起来应用，其效果会更显着。
6．双重抽样 调查某一种不容易观察测定的、耗费甚大的、用较多时间的、必须破坏性测定等才能观察到的复杂(直接)性状，而且要直接获得这种性状是困难的。必须设法找出另一种与该复杂性状有密切相关关系且比较容易观测的简单(间接)性状，利用这两种性状客观存在的关系，通过测定简单性状结果从而推算复杂性状的测定结果。抽样调查的做法是要求随机抽出两个样本。第一个样本具有少量的抽样单位。例如，n个单位，测定所要调查的两种性状。假定以y代复杂性状作为依变数，以x代简单性状作为自变数。这样一个样本就获得n对x和y数据。第二个样本具有比之前者较多的抽样单位。例如，m个单位，而m＞n。这个样本仅观测简单性状，获得m个x性状数据。倘从第一个样本中测验这两种性状之间存在有显着相关，那么，可以根据直线方程计算求复杂性状对于简单性状的回归方程式如下：
b代表回归系数。倘从第二个样本计算简单性状较为精确的平均数以
代表，那么，可用这个平均数
代上式的x值，以估计相应于第二样本具有较大容量(即m)的复杂性状平均数(
)值。
这种抽样方法叫做双重抽样。
双重抽样有如下优点：
一是对于复杂性状的调查研究，可以通过仅测定少量抽样单位而获得相应于大量抽样单位(指在第二个样本)的精确度，从而节约时间、人力和物力。
二是当复杂性状必须通过破坏性测定才能调查时，则仅有这种方法可以采用。例如，从玉米茎上的蛀孔数(简单性状)推算玉米螟的幼虫数(复杂性状)；如以玉米螟的高峰期卵块数来推算百株累计卵块数；又如在甘薯生长期中，估计甘薯小象甲为害程度，要把甘薯挖出检查，这样会损耗很大。但用薯片诱测等方法，依薯片诱虫密度与为害程度的相关关系来作将来甘薯为害损失的估计。
(二)抽样误差的计算 抽样误差的概念已在前面阐述过。上述抽样误差的计算方法、计算公式及其例子均属纯随机抽样方式，在此不再赘述。现将其他主要抽样形式的抽样误差计算方法简述如下。
1．类型抽样 类型抽样的抽样误差取决于各组样本单位数(n)和各组组内标准差平方或各组组内方差的平均数(
)。因此，类型抽样的抽样误差公式应为：
重复抽样条件下：
上式两边除以t，即可得如上计算公式。
上式两边除以t，即可得如上计算公式。
不重复抽样条件下：
式中 P(1－P)——各类型组的Pi(1－Pi)的加权算式平均数；
Pi——各类型组的样本成数。
2．整群抽样 其误差计算方法与上述类型抽样的抽样误差计算方法正好相反，即不是用组内平均方差而是由组间方差代替纯随机抽样误差计算公式中的总体方差来计算的。由于整群抽样不采用重复抽样，因此，下面仅介绍不重复抽样条件下的整群抽样误差公式。
整群抽样平均指标的抽样误差为：
式中 
——群间方差，即各群子总体平均数对总体平均数的标准差平方，用公式表示：
若资料缺乏时，可用样本资料估计；
R——总体的群体个数；
r——样本的群体个数。
若R值较大时，整群抽样平均指标的抽样误差可简化为：
整群抽样成数抽样误差为：
式中 
——成数指标的群间方差，即各群总体成数对总体成数的标准差平方，用公式表示：
若资料缺乏时，可用样本资料估计，其他符号相同。
若R值较大时，上述误差公式可简化为：
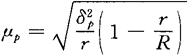
现举例说明整群抽样时抽样误差的计算方法。
例如，某县病虫测报站调查晚稻秧田的稻瘿蚊为害率，共6块田，面积2800m2，每块田随机取样5点，每点查0．1m2，结果平均标葱率为20%，样本群间方差为4．71%，则抽样误差的计算如下：
第一步，确定总体群数和样本群数，该乡调查6块田，面积为2800m2，每0．1m2为一群体。这样可将总体分为总群体数28000个，即R=2800÷0．1=28000(个)，每块田抽取5个群体，总体即有抽样群体30个，即5×6=30(个)；
第二步，将有关数字代入抽样误差公式，得
若按73．3%概率把握程度，则平均为害率为：
∵ P－t·μp≤P≤p+t·μp
∴ 20%－1．11×4．0%≤P≤20%+1．11×4．0%
15．56%≤P≤24．44%
计算结果表明，标葱率在15．56%至24．44%之间，有73．3%的把握程度。
3．机械抽样 若直接计算抽样误差是一个相当复杂的问题，一般都采用间接方法来处理。机械抽样，如按无关标志排列总体单位的顺序，其抽样误差与纯随机抽样误差就十分接近，所以通常采用纯随机抽样误差的计算公式来代替；若按有关标志排列顺序的，则采用类型抽样的抽样误差的计算公式来代替。
五、抽样资料的推算
(一)抽样资料推算的意义 抽样资料的推算又称为抽样估计。这是抽样调查的基本任务。所谓抽样资料的推算，是根据抽样取得的样本指标，采用一定的估计方法，估计推算相应的总体指标的方法。用样本指标估计总体指标时，涉及到样本估计值、抽样估计允许误差和允许误差置信度三个基本要素。为此，要弄清其概念和计算方法。
样本估计值，是指根据抽样调查的目的，为推算某个总体指标数值采用某个样本指标的数值。在抽样推算中，一般用样本平均数或样本成数作为总体平均数或样本平均数的样本估计值。
抽样估计的允许误差，是指根据抽样调查的客观条件的要求允许存在的样本估计值的误差范围，也是指抽样指标和总体指标之间抽样误差的可能范围。其基本公式是：
，△p=t·μp
式中 
与△p分别表示抽样平均数和抽样成数的误差范围。
若结合抽样平均误差的计算公式，允许误差的计算公式还可以表示如下。
重复抽样条件下：
不重复抽样条件下
若以样本标准差S和样本成数P作为总体标准差δ和总体成数P的样本估计值，则有：
重复抽样条件下：
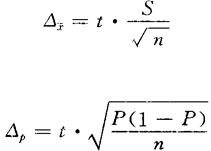
不重复抽样条件下：
一般情况下，允许误差的置信度是随允许误差的变化而变化的。允许误差愈大，允许误差的置信度就愈大，反之就愈小。
(二)抽样代表性检查 抽样的目的在于通过抽样指标推算全及总体指标。然而，要获得较为理想的而且能客观地反映全及总体指标，保证抽样结果能够获得代表性的资料，往往需要进行抽样代表性的预先检查。就是说，根据已掌握的资料，推算出全及总体的某些综合指标，然后和抽样总体均同一指标相比较。
所谓已掌握的资料，就是利用某一次(含过去)调查结果的平均值。如果过去缺乏上述有关资料，作一般性的粗略地检查和判断。
在上述比较过程中，通常将抽样总体的指标和已掌握的全及总体同一指标的比率用百分数形式表示。用这个比率来说明抽样代表性的程度，一般不超过5%。若对比结果不超过5%，表示这个比率落在95%－105%之间，一般可以认为抽样代表性是令人满意的。如果超过这个范围，就需要重新抽选，再次抽选仍未得到满意的结果，不再重新抽选，而是在原来抽样基数的基础上，增加抽样单位，直至达到满意为止。例如，某县在全县20个乡中确定样点乡5个。根据调查结果，样点乡的水稻稻飞虱加权平均百丛禾有虫分别为500头、650头、700头、730头、760头。被抽中的样点乡平均百丛禾虫量为：
(500+650+700+730+760)÷5=668(头)
据全县20个乡抽样调查，全县平均百丛禾虫量为701头。
上述两个平均百丛虫量的比率为：701÷668=1．0494或104．94%。由此可见，其比率没有超过5%。这说明了被抽中的5个乡是具有代表性的。
(三)抽样资料的推算 抽样资料的推算方法，是指根据抽取的样本资料(指标)来估计总体指标(如平均数、标准差、比率等)的方法。通常采用点估计和区间估计两种。
1．点估计也称定值估计 是指以实际抽样调查资料得到的指标
与p直接估计相应的总体
或P的一种抽样估计方法。例如，从1000kg棉籽中，随机抽取10个点共10kg棉籽进行检查，结果得棉铃虫1头。由此可直接推断这批棉籽平均每公斤有棉铃虫0．1头，则含虫率为10%。
点估计的方法比较简单，只有在对被估计的对象要求严格的情况下才有使用价值。因为这种做法没有考虑抽样误差，亦没有说明有多大的准确度和估计把握程度。
2．区间估计 此法是根据样本指标
或p、抽样误差μp去推断总体指标的可能出现的范围。与点估计相比较，可明显地看出，推断方法是间接的推断而不是直接推断。但它能够说清楚估计的准确度和把握程度，有应用价值，而且是抽样估计中的主要方法。现又以上例来说明，总体指标(1000kg)和样本指标(10kg)，与上例相同，但其棉铃虫含量不是平均值而是8%－12%之间，并且标出把握程度有多大(比如90%)。所以，此法是抽样估计中的主要方法。然而，要做好区间估计，应掌握如下三个要点：
一是根据样本指标和抽样误差计算总体指标所在的可能范围。其计算公式为：
平均指标：
成数指标：p－△p≤P≤p+△p
由此可见，这种估计方法有一个上限和一个下限，并由它们组成一个区间。上式平均数的下限为
，上限为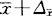
；成数区间估计的下限为p－△p，上限为p+△p。
二是区间估计所表示的为一个可能的范围，而不是一个绝对可靠的范围。因为区间估计是涉及到抽样误差，而实际上抽样指标和总体指标的绝对值是不可能求得的。用抽样指标准确无误地推断总体指标可能性是极小的。所以，进行区间估计的意义在于不仅给出总体指标存在的范围，而且给出总体指标在这个范围内的置信度或概率把握程度。由于△x=t·μx，△p=t·μp，所以区间估计的一般公式可以表示为：
p－t·μp≤P≤p+t·μp
例如，在上例中，棉籽平均含棉铃虫率为10%，抽样误差为2%，若要求估计把握程度为68．27%，则查概率表t为1，那么△p=1×2%=2%，于是该批棉籽平均含虫率的区间为：
10%－1×2%≤P≤10%+1×2%
即： 8%≤P≤12%
因此，该批1000kg棉籽平均含虫率将在8%－12%之间，把握程度为68．27%，亦就是说1000kg棉籽的含虫率包括在这个区间的可靠性是68．27%。
三是扩大或缩小抽样误差的范围可以提高或会降低推断的把握性。
譬如，在上例中，若将估计的误差范围扩大1倍，所以△p=2×2%=4%。
则： 10%－4%≤P≤10%+4%
即： 6%≤P≤14%
因此，该批的1000kg棉籽平均含虫率将在6%－14%之间，这时由于t=2(由于t=误差范围／平均抽样误差=4%÷2%=2)，查概率表得F(t)为95．45%，即把握程度可达到95．45%。
若将估计的误差范围缩小1倍，所以△p=0．5×2%=1%，则：
10%－1%≤P≤10%+1%
即： 9%≤P≤11%
因此，该批的1000kg棉籽平均含虫率将在9%－11%之间，这时由于t=0．5，查概率表得F(t)为38．29%，即把握程度低，降到38．29%。