回归预测法

出处：按学科分类—经济 企业管理出版社《现代企业内部会计实用手册》第959页（5942字）

回归预测法包括一元回归预测法和多元回归预测法等，下面分别讨论。

一、一元回归预测法

为对某一量的未来状况作出预测，通常可在对其有影响的(或与其相关的)多个因素中，选择一个基本的、起决定作用的因素作为自变量，而把作为预测对象的变量视为因变量；自变量可用x来表示，因变量用Y来表示。如果用线性函数Y=α+Bx来表述二者的关系，就说是线性回归，否则，如果用某种非线性函数如Y=α+β或函数Y=αxβ来表现Y与x的关系。便说是非线性回归。对于具体问题，究竟用那种函数形式为好，需要酌情而定，一般要求，所用的函数应最能反映变量的真实关系。

现仅就线性回归说明这一方法。这是因为线性回归理论比较成熟，同时，有些非线性函数如Y=α+β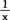又可以变换成线性函数形式。如令Z=，便有Y=α+βZ，这正是线性函数，可仿照线性回归方法进行处理。

仍用Y₁，Y₂，…，Y_n表示变量Y的观测值(但不一定是按时间顺序排列的)，用x₁，x₂，…，x_n表示与诸Yi对应的变量x的观测值；事实上也可以写成(Y₁，Y₁)，(Y₂，Y₂)…，(Y_n，Y_n)，它们一起作为变量Y和X的n组观测值，来确定直线函数Y=α=βX中的参数α和β的值，使得直线方程=+X为样本点(Y₁，X₁)，(Y₂，X₂)，…，(Y_b，Y_b)分布的最佳拟合如图表3－8所示，这里，称，为参数α和β的估计值。

图表3－8

显然，这同配合直线的方法是极相似的。事实上，求参数的方法和计算参数的公式也都相似。只不过以前讲的是t_i，这里是X_i。

从而得到和的计算公式：

下面用例子来说明线性回归方程的求法及其应用。

〔例〕某市电子工业公司所属14个企业中，各企业的年劳动生产率(Y)和年设备能力(X)统计数据如图表3－9所示。

图表3－9

图表3－10

从上图可见，用直线函数Y=α+βx来表现Y与X的关系是合适的。于是可通过建立直线回归方程=+x，作出预测。为此先计算，，列计算表如下：

图表3－11

据上表可见，∑Y_i=132．9，∑Y_i=61．8，∑Y_iX_i=622．81，∑X=296．8，n=14，将其代入公式，便得：

于是，所要求的回归方程为：

Y=3．1003+1．4481X

再根据此方程预测因变量Y的数值时，需先给出(或测出)X的值，然后将其代入方程求解。如假定该公司准备对某一企业进行设备改造，改造后的年设备能力可达9．24瓦／人。则据上述方程便可预测出该企业的年劳动率将为：

Y=3．1003+1．4481×9．2=16．4(千元／人)

以上我们介绍了线性回归方程的求法，以及在预测中怎样使用它。需要进一步说明的是，对Y与X实行线性回归，或用Y=α+βX来表现二者之间依存关系，具有很大的假定性(因为Y与X也可能不具有此线性关系)这样做的目的，是想通过X的变动来测定Y的变动，或是要用X来“说明”Y。但是，变量Y与X是否相关，相关程度为何仍然是未知的。为了对此种相关性进行考察，我们引进了相关系数。

相关系数常用r表示，其定义是：

r为介于－1和+1之间的数；r＞0时，说明变量Y与X具有正相关，r＜0时，说明Y与X有负相关，r=0，则称二者无关。r的绝对值越近于1，表明相关程度越密切。一般，只要r的绝对值大于0．85就说Y与X具有高度相关。

以上例为例，来计算劳动生产率Y和设备能力X的相关系数。计算相关系数r所需计算的各项(如∑Y_i，∑X_i，∑Yi²等)数值在图表3－11中均已完成，只需将有关的计算结果代入公式中即可，则有：

根据这一结果，可以认为劳动生产率(Y)与设备能力(X)具有高度相关。

二、标准差与区间预测

以上介绍了一元线性回归预测基本方法。接下来我们引入标准差的概念，利用它还可进行区间预测。

我们知道，根据Y对X的回归方程式=+X，只要将X的值代入，就可以求出变量Y的预测值_。自然地，如果用X的样本观测值X₁，X₂，…，X₁代入其中，又可以求出Y的样本观察值Y₁，Y₂，…，Y_i的估计(预测)值，记为，，…，。一般说来，由于因变量Y还受自变量X以外的其他因素的影响，诸Y_i与_i之间常常存在着偏差，即Y_i－_i常常是不等于0。为了衡量此种偏差的程度，我们令：

则为误差平方和∑(Y_i－_i)²的平均值的开平方，我们称其为标准估计误差，简称标准差。显然，＞0，而且其数值大小，体现了偏差的程度，也反映回归方程的性能。

再以前例为例来计算。我们可先将X的样本观测值分别代入回归方程式=3．1003+1．4481X，求出Y的样本估计值。如将X_i=2．8代入，就可求出=3．1103+1．4481×2．8=7．15，以此类推。然后，再按公式的要求计算出所需的数值，详见图表3－12(表中第三栏数字即为Y的样本估计值)。

图表13－12

据上表知，∑(Y_i－_i)²=2．0067，而n=14，这样，代入公式便得：

利用标准差便可进行区间预测。我们用Y表示预测时期变量Yf的真值，用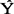_f表示用某种方法计算出Yf的预测值。根据统计学原理可知：

(1)Y_f值在_f的一个标准差(±)范围内，即在〔_f－，_f+〕之间的概率为68．7%。

(2)Y_f值在_f的二个标准差(±2)范围内，即在〔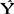_f－2，_f+〕之间的概率为95．45%。

(3)Y_f值在Y_f的三个标准差(±3)范围内，即在〔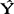_f－3，_f+3〕之间的概率为99．73%。

例如，我们曾求出设备能力为9．24瓦／人，企业的年劳动生产率为16．4(千元／人)。

亦即_f=16．4。那么，我们就可以说，设备能力为9．2(千瓦／人)时企业的年劳动生产率在〔16．4－2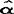，16．4+2〕的概率为95%。或者说，该企业的劳动生产率有95．45%的可能，在

〔16．4－2×0．3785，16．4+2×0．3785〕即在15．643～17．157之间。

三、多元线性回归预测法

为了更准确地预测出某一量的未来水平。往往只用一个自变量来说明预测变量是不够的，而应用时考虑多个因素对预测变量的影响，即进行多元回归。譬如，要更准确地预测家俱量的未来需求水平，就可以同时考虑新建住房面积、新婚户数、居民货币收入、以及价格等因素。这样，可以从不同侧面对预测变量的可能变动加以反映。

多元回归也有线性和非线性回归之分。但最常使用的是多元线性回归方法。多元线性回归的回归方程式可一般表示为：

Y=β₀+β₁X₁+…β_kX_k

式中，Y为因变量，X₁，X₂，…X_k为k个自变量，(注意：且不可将此记号同一元回归场合的样本值相混淆)，β_。，β₁，…，β_k为参数。

进行多元线性回归的主要问题，仍在于利用各个变量的样本观测值，求参数的估计值，建立起回归方程。其基本过程与一元回归是类似的。下面仅以二元线性回归为例，说明回归方程的求法。

二元线性回归的方程式为：

Y=β₀+β₁X₁+β₂X₂

利用最小二乘法将可证明，β₂，β₁，β₂的估计值_。，1_，2可由下面的三元一次方程组解出。

〔例〕为对某手表公司的销售额(Y)作出预测，考虑以营业人员数(X₁)和所支出的推销费用(X₂)为自变量。并用线性函数Y=β_。+β₁X₁+β₂X₂来表现三者的依存关系。图表13－13为各变量的统计数据(观测值0在该表的后半部分列出了求参数估计值时所需计算的各项结果。

图表13－13

据上表可见，∑Y1=2252，∑X_i1=2432，∑_i1=1406，∑Y1X_i1=689492，∑_ii1=397．385，∑_i1i2=322943，∑X=744．312，∑X_i2²=218056，n=8。将这些数据代入公式得：

2252=8₀+2432β₁+1506₂

689492=2432₀+744312₁+322943β₂

397．385=1406₀+322943β₁+218056β₂

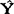解此方程组就可得到₀=－98．2457，₁=0．6396，₂=1．0537，从而，回归方程为：=－98．2457+0．6396X₁+1．0537X₂。

该方程可称为是，手表销售额(Y)关于营业人员数(X₁)和推销费用(X₂)的二元线性回归方程。当用其预测时，只需将同时期的X₁和X₂的值代入，计算出该时期的。如假定该公司计划1994年增加营业人员，总数可达310人，同时将推销费用增加到250万元，那么，该年该公司的销售额将为：

1984=－98．2457+0．6396×(310)+1．0537×(250)=363．45(亿元)

在多元线性回归场合，为考察每个变量与因变量的相关程度，可分别计算各自的偏相关系数。然而，更为重要的是计算复相关系数，因为它可以考察全部自变量一起与因变量的相关程度。从而可从总体上鉴定回归方程的性能。

复相关系数一般用R表示，其定义是，

式中，，_i为按回归方程计算的Y_i的估计值，(i=1．2，…，n)。现结合上例说明复相关系数R的求法，见图表13－14。

图表13－14

据上可得知，∑(Y₁－_i)²=16．43，∑(Y_i－)²=4818，从而有：

这表明，所用的两个自变量却与因变量有较密切的相关，用这两个变量建立的回归方程性能比较好。

对于这个例子，我们也可进行区间估计。首先，据图表13－14可计算出标准差。

而已求得1994年的预测值为_f=363．45(亿元)。那么，则有：

Yf±2α=363．45±2×1．433=363．45±2866

从而得95．45%的置信区间为：

〔360．58，366．32〕

即，该公司1994年的销售额Y₁，有百分之九十五以上的可能，在360．58亿元至366．32亿元之间。