某厂曲轴的二元回归分析

出处：按学科分类—经济 企业管理出版社《现代企业内部会计实用手册》第1086页（2041字）

曲轴是柴油机的主要零件之一，柴油机的回转运动主要通过连在曲轴上的连杆带动活塞往复运动而产生，因而曲轴需要承受较大的扭矩。任何微量的变形，都会导致曲轴轴颈与连杆轴承产生过热现象而磨损，从而影响柴油机正常工作。曲轴加工精度较高。因此，提高曲轴质量是保证柴油机质量的前提。

主轴颈键槽中心与连杆轴颈中心的偏差是反映曲轴质量的两个重要指标。这两个变量自身的偏差程度，直接影响主轴中心和曲拐中心的偏移度，而变量之间又无法用函数表达式表达，因此，要控制偏移度，可以轴颈键槽中心和曲拐中心偏差进行回归分析。

由于相对因变量y(偏移度)而言存在两个自变量9键槽中心与连杆轴颈中心)，所以，通常采用二元回归分析法来分析它们之间的线性相关关系。

设主轴颈键中心偏差为自变量x₁，连杆轴颈中心偏差为自变量x₂，轴心偏移度为因变量y。将测得的x₁、x₂、y值的数据列于表1。

表1

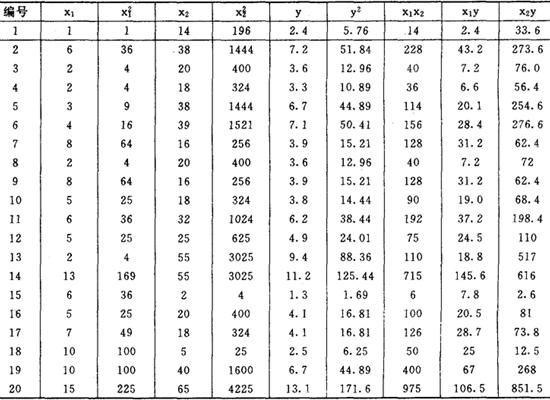
按照表1中所列观测值数据及中间值计算数据，运用最小二乘法原理确定二元归方程y=b₀+b₁+b₂x的系数值，使方程与所有观测数据误差的平方和Q=∑(y－y)₂达最小值。

计算步骤如下

用正规方程求解回归系数

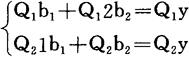
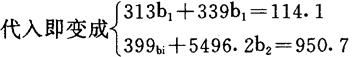
解方程得

b₁=0．1857 b₂=0．1615

常数项b₀=yb₁x₁－b₂x₂=5．1145－0．1587×6－0．1615×27．7=0．0242将回归系数代入

y=b₀+b₁x₁+b₂x₂

得 y=0．0242+0．1587x₁+0．1615x₂

即所求之二元回归方程。

因为自变量和因变量都是随机变量，所以，可通过求出密切程度指标r_f及从方差分析表2分析出主轴中心与曲轴中心偏度y对自变量x₁ x₂的线性相关和密切程度及回归显着程度，从而有效地加以预测和控制。

表2

二元回归方差分析表

复相关系数

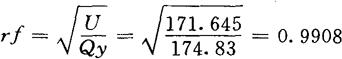
取a=0．05，v₁=2，v₂=17时

查F表知F_0．05=3．59

取a=0．01时

查F表知F_0．01=6．11

结果统计量F＞F_。．0_1，

这就说明回归是高度显着的，且相关程度达99%。

由于测量键中心与曲轴中心夹角目前缺乏测试手段，所以要控制质量特性值y，可通过控制两个自变量x1与x2的值来达到。

而对y值的评估，就要通过求出剩余标准差s的值，使偏移度y取值范围分布在b₀±2_s+b₁x₁+b₂x₂两条回归直线之间。

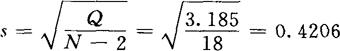
取置信系数1－a=0．95(即落在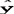±2s之间的分布概率为95%)，

Y′=b₀+2s+b₁x₁+b₂x₂

=0．8654+0．1587x1+0．1615x2

Y″=b₀－2_s+b₁x₁+b₂x₂

=－0．187+0．1587x₁+0．1615x2

按照上下界限回归直线区间，如果将主轴颈键槽中心偏差控制在5，曲轴中心偏差控制在28范围内，其中心偏移度有95%可以处于4．498～6．18状态下。这样，就能把曲轴的质量控制在自己手里。