函数

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第20页（2839字）

邻域 设a与δ为两个实数，且δ＞0，数集｛x||x－a|＜δ｝称为点a的δ邻域，点a叫做这个邻域的中心，δ叫做这个邻域的半径，记作

U_δ(a)=｛x||x－a|＜δ｝=｛x|a－δ＜x＜a+δ｝．

数集｛x|0＜|x－a|＜δ｝称为点a的去心δ邻域，记作U_δ(a)．

函数 设x和y是两个变量，D是一个给定的非空数集，如果对于每个数x∈D，变量y按照一定法则总有确定的数值和它对应，则称y是x的函数，记作y=f(x)．

数集D叫做这个函数的定义域，y叫做因变量，x叫做自变量．

单值函数 如果自变量在定义域内任取一个数值时，对应的函数值总是只有一个，这种函数叫做单值函数，否则叫做多值函数．

分段函数 在自变量的不同变化范围内，对应法则用不同的式子来表示的函数，称为分段函数．例如：

取整函数 设x为任一实数．不超过x的最大整数称为x的整数部分，记作［x］．这个函数称为取整函数．

反函数 设函数y=f(x)，当变量x在一个区域D内变化时，变量y在区域W内变化，如果对于变量y在区域W内任取一个值y₀，变量x在区域D内有x₀，使y₀=f(x₀)，x=φ(y)，则变量y是变量x的函数，函数x=φ(y)称为函数y=f(x)的反函数，二者图形是相同的．习惯上自变量用x表示，因变量用y表示．因此也可以说y=φ(x)是y=f(x)的反函数，原来的函数y=f(x)称为直接函数．这时直接函数与反函数的图形关于直线y=．x对称．

有界性 若，存在M＞0，对任意x∈X有|f(x)|≤M成立．则称函数f(x)在X上有界，否则称f(x)无界．

单调性 设函数f(x)的定义域为D，区间I∈D．如果对于区间I上任意两点x₁及x₂，当x₁＜x₂时，恒有f(x₁)＜f(x₂)，则称函数f(x)在区间I上是(严格)单调增加的；如果对于区间I上任意两点x₁及x₂，当x₁＜x₂时，恒有f(x₁)＞f(x₂)，则称函数f(x)在区间I上是(严格)单调减少的．

单调增加和单调减少统称为单调函数．

奇偶性 设函数f(x)的定义域D关于原点对称，如果对于任意x∈D有f(－x)=f(x)恒成立，则称f(x)为偶函数；

如果对于任意x∈D有f(－x)=－f(x)恒成立，则称f(x)为奇函数．

周期性 设函数f(x)的定义域为D．如果存在一个不为零的数l，使得对于任－x∈D有(x±l)∈D，且f(x+l)=f(x)恒成立，则称f(x)为周期函数．l称为f(x)的周期，通常说的周期函数的周期是指其最小正周期．

基本初等函数

(1)幂函数(见图2．1) y=x^μ (μ是常数)．

图2．1

(2)指数函数(见图2．2) y=a^x (a＞0，a≠1)．

图2．2

(3)对数函数(见图2．3) y=log_ax (a＞0，a≠1)．

自然对数函数：y=lnx．

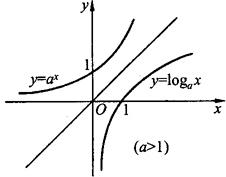
图2．3

(4)三角函数(见图2．4)

图2．4

正弦函数：y=sinx，余弦函数 y=cosx，

正切函数；y=tanx，余切函数 y=cotx，

正割函数：y=secx，余割函数 y=cscx．

(5)反三角函数(见图2．5)

图2．5

图2．5(续)

反正弦函数：

反余弦函数：y=arccosx，x∈［－1，1］，y∈［0，π］；

反正切函数：；

反余切函数：y=arccotx，x∈(－∞，+∞)，y∈(0，π)．

复合函数 设函数y=f(u)的定义域为D_f，而函数u=φ(x)的值域为Z_φ，若，则称函数y=f［φ(x)］为x的复合函数．其中x为自变量，u为中间变量，y为因变量．

初等函数 由常数和基本初等函数经过有限次四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数，称为初等函数．

双曲函数(见图2．6)

图2．6

双曲函数常用公式

sinh(x±y)=sinhxcoshy±coshxsinhy；

cosh(x±y)=coshxcoshy±sinhxsinhy；cosh²x－sinh²x=1；

sinh2x=2sinhxcoshx；

cosh2x=cosh²x+sinh²x．

反双曲函数