三角高程测量

出处：按学科分类—工业技术 中国建材工业出版社《工程测量实用技术手册》第88页（2558字）

1．三角高程测量原理

三角高程测量原理是根据两点间的水平距离及竖直角应用三角学公式计算两点间的高差。三角高程测量主要用于测定图根控制点之间的高差，尤其在测区进行三角高程测量的先决条件为两点间水平距离已知，或用光电测距仪测定距离。如图5－19所示，欲测定A、B两点间的高差，安置经纬仪于A点，在B点竖立标杆。设仪器高为i，标杆高度为v，已知两点间平距为D，望远镜瞄准标杆顶点M时测得竖直角为α，从图中看出高差h_AB公式为

h_AB=Dtanα+i－v

已知A点高程为H_A，则B点高程H_B公式为：

H_B=H_A+h_AB

上述三角高程公式推导是假设大地水准面是平面，事实上，大地水准面是曲面，因此，还应考虑地球曲率对高差的影响。当距离大时，地球曲率的影响不可忽视，从图5－20中看出高差值应增加c，c称球差改正。另外，由于大气折光的影响，测站望远镜观测目标顶点M的视线是一条向上凸的弧线，使α角测大了，从图中看出高差值中应减少γ，γ称气差改正。

图5－19 三角高程测量原理

图5－20 三角高程测量原理(长距离)

从图5－20中看出：

h_AB=NP+PQ－NB

上式中：NP=Dtanα，PQ=i+c，NB=v+γ，代入后得：

h_AB=Dtanα+i+c－(v+γ)

即

h_AB=Dtanα+i－v+(c－γ)

上式为三角高程测量计算公式，式中(c－γ)即为球差与气差两项改正。

球差改正c为：

式中 R——地球曲率半径；

D——两点间水平距。

大气垂直折光影响使视线变弯曲，其曲率半径R′为变量，设，称为大气垂直折光系数，它受地区高程、气温、气压、季节、日照、地面覆盖地物和视线超过地面的高度等诸多因素的影响。通常认为R′7R，将其代入折光系数公式得

仿照式可写出气差改正的公式

从式h_AB=Dtanα+i－v+(c－γ)看出：球差改正c恒为正，气差改正γ恒为负。球差改正与气差改正合在一起称为两差改正f，即

因此，三角高程测量计算式可写为：

h_AB=Dtanα+i_A－v_B+f

可以看出，当D越长，两差改正越大，当D=1km时，f=6．7cm。因此，三角高程测量一般采用往返观测，又称对向观测，取往返平均值可以消除两差的影响。因为

由A站观测B点：

h_AB=Dtanα_A+i_A－v_B+f

由B站观测A点：

h_BA=Dtanα_B+i_B－v_A+f

往返取平均得：

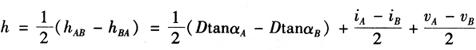
从上面公式可看出两差自动消除了。

2．三角高程测量观测与计算

(1)三角高程测量观测

在测站上安置经纬仪(或全站仪)，量取仪器高i，在目标点上量实标高，或安置棱镜，量棱镜高v，仪器高i与目标高v，用皮尺量，取至厘米。

用正倒镜中丝观测法或三丝观测法(上、中、下三丝依次瞄准目标)观测竖直角。注意正倒镜瞄准目标时，目标成像应位于纵丝左、右附近的对称位置。竖直角观测测回数与限差按表5－12规定。

表5－12 竖直角观测测回数与限差

(2)三角高程测量的计算

三角高程测量往测、返测根据前文介绍计算。往返高差较差的容许值△h_容，对于四等光电测距三角高程测量规定为：

式中 D——两点间的水平距离(km)。

图根三角高程测量对向观测两次高差的校差，城市测量规范规定应小于或等于0．4×D(m)，D为边长，以km为单位。

如图5－21所示的三角高程测量控制网略图，在A，B，C，D四点间进行了三角高程测量，构成了闭合线路。已知A点的高程为450．56m，已知数据及观测数据注于图5－21上。计算列于表5－13和表5－14中。

图5－21 三角高程测量控制网略图

表5－13 电磁波三角高程测量高差计算

表5－14 三角高程测量高差调整及高程计算

由对向观测所求得高差平均值，计算闭合或附合线路的高差闭合差f_h的容许值，对于四等光电测距三角高程测量来说同四等水准测量的要求，在山区为：

式中 D_i——相邻两点之间的边长。