不可展曲面构件的展开

出处：按学科分类—工业技术 江苏科学技术出版社《铆工实用技术手册》第211页（7648字）

环面、球面、螺旋曲面等均为曲线表面，它在两个方向同时弯曲。由于曲纹表面上不存在直素线，它的两条相邻曲素线不可能构成一个平面，所以是不可展表面。扭曲面和单叶双曲面虽然是由直素线组成，但其相邻两条线是异面直线，既不平行也不相交，因而也是不可展表面。这些不可展表面不可能按其实际形状和大小不变形地依次摊平成平面，因此在生产实际需要时只能进行近似展开。

近似展开的方法，一种是把不可展曲面分成若干个曲面三角形，然后将它们近似地作为平面三角形来展开；另一种是将曲面分成若干部分，然后把它们近似于某种可展曲面来展开。

1．等径直角换向接头的近似展开

如图3－86所示为一等径直角换向接头(也称压制弯头或争气弯头)的两投影及其展开图。该曲面是一柱状面，由于柱状面的相邻两素线是交叉的，所以它是不可展表面。如果所取相邻两素线间的距离特别小，则两素线之间的曲面可近似地看成为一个平面四边形，且每一四边形又可分为两个三角形，故画换向接头的近似展开图可应用三角形法，具体作图步骤如下：

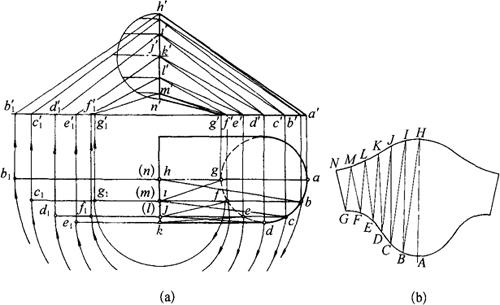
图3－86 等径直角换向接头的近似展开

①把导线圆分成若干等份(本图为12等份)，且将它们的对应点连接起来，如AH、BI等，由于换向接头的形状前后对称，故图上只画出了前面的一半。

②把两素线间的曲面(如ABIH)近似地看成平面四边形，连接其对角线BH，分四边形ABIH成三角形ABH和三角形BHI。

③线段AH、BI是正平线，其正面投影a′h′、b′i′反映实长。弧AB及HI等长，用弧长ab近似地代替，对角线BH为一般位置直线，用旋转法求出其实长后，就可在展开图上画出三角形ABH及三角形BHI，即得四边形ABIH的展开图。

④用同样方法画出其余部分的展开图，用曲线光滑连接所得各点，即得到换向接头表面的近似展开图，如图3－86(b)所示。

2．正螺旋面的近似展开

圆柱形螺旋输送机又名搅龙，可用来输送颗粒状、粉末状等物质，也可以作搅拌机构，用途较广。在加工制造时，需将螺旋叶片焊接在机轴上。它与螺纹一样有单、双线，左、右旋之分。单线螺旋周节等于导程；双线螺旋周节等于1／2导程。螺旋叶片一般按一个导程或稍大于一个导程的螺旋面展开下料，胎曲成形后把若干个螺旋面拼接成整体搅龙。除专门生产螺旋输送机的工厂外，一般工厂均用圆柱螺旋面作为搅龙的叶片。现介绍正圆柱螺旋面近似展开的方法。

(1)三角形法

圆柱螺旋面为不可展曲面，只可用近似的方法展开。也就是把螺旋面分成若干三角形面，然后求出这些三角形的边长，再依次画出它们的实形。具体作图步骤是：

①用圆柱螺旋面的内外直径d、D画出俯视图，12等分俯视图大小圆周，等分点为1、3、5、…、13、0、2、4、…、12，用点划线和实线交替连接各点。在主视图取12等于导程，并作12等分。由等分点引水平线，与从俯视图大小圆周等分点所引上垂线所得的对应交点分别连成两条螺旋曲线，完成主视图，如图3－87所示。

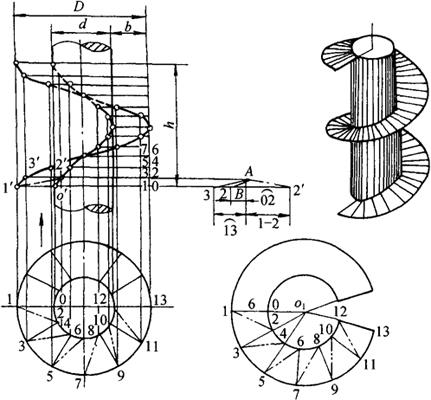
图3－87 正螺旋面的近似展开

②求实长，作展开。由主视图和俯视图可明显看出螺旋面上各三角形的实线边为水平线，其水平投影反映实长，且各线实长相等；各点划线及大小圆的等分弧是一般位置直线和曲线，各线的两面投影均不反映实长，可用直角三角形法求出。如实长图，取B2、B3、B2′等于俯视图的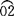、、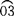1－2，取AB等于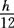，连接A2、A3、A2′为俯视图两圆等分弧所对应的螺旋线及各点划线的实长。再用各实长线作出展开图。

(2)简便展开法

如图3－88所示，一个导程的圆柱螺旋面的展开图是一环形切口圆。若已知正螺旋面的外径D、内径d和导程h，可用简便法作展开图。用简便法展开，不用画螺旋面的投影。其具体作法为：

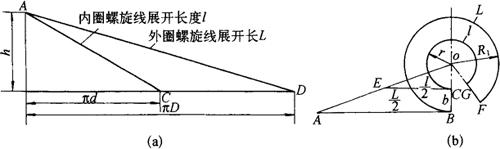
图3－88 正圆柱螺旋面近似展开的简便画法

①用直角三角形法求出内外螺旋线的实长l及L。

②作一直角梯形ABCE，使AB等于L／2，CE等于l／2，BC等于1／2(D－d)，且AB平行于CE，BC垂直于AB。连接AE、BC，并延长两线相交于0。

③作展开。以o为圆心，0B、oC作半径画同心圆弧，取等于L，连接Fo交内圆弧于G，即得所求展开图。

(3)计算法

由图3－88得知

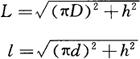
若环形圆的内、外半径以r、R₁表示，则

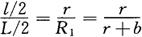
l(b+r)=Lr lb=r(L－l)

所以

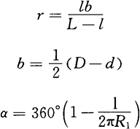
【例13】 设圆柱螺旋面的外圆直径D=310mm，内径d= 140mm，导程h=300mm，试用计算法求出展开图的主要参数，并作展开图。

解：

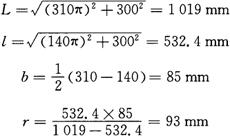
R₁=85+93=178mm

根据以上各式求出的值，即可作出展开图，如图3－89所示。在实际放样中，圆柱螺旋面的展开图一般不作扇形切口，而是完整的环形图，这时的螺旋面稍大于一个导程。

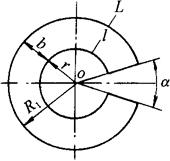
图3－89 正圆柱螺旋面计算展开的主要参数

3．球表面的近似展开

球面是曲线表面，它在两个方向同时弯曲，故不能自然地展开成为平面，为典型的不可展曲面，只能作近似地展开。假如不可展曲面构件的表面是由许多小块板料拼接而成，且每一小块板料是单向弯曲可展的，于是整个球面就被近似地展开。把各小块下料成形拼接便完成整个球体。

球面分割方式一般有分块法和分带法两种。球表面等分数愈多球面愈光滑，但相应的落料成形愈频繁。等分数的多少应依据球直径大小而定。

(1)球面的分瓣展开

球面分瓣法是沿径线方向分割球面为若干块，每块大小相同，展开图为柳叶形，如图3－90所示。其具体作法为：

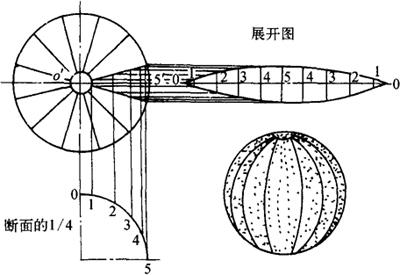
图3－90 球面的分瓣展开

①用已知尺寸和12块板料等分数画出有极帽的主视图和1／4断面图。四等分断面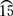圆弧，等分点为1、2、3、4、5。从等分点向上引垂线得与结合线交点。

②作展开。在向右延长的水平轴线上截取00等于断面图半圆周长，且由中点5向左右照录断面图4、3、2、1点。通过各点引垂线，和从结合线各点向右所引水平线得对应交点分别连成光滑曲线，便得球面展开图的1／2。

(2)球面的分带展开

球面分带法是沿纬线方向分割球面为若干横条带，横条带的数量多少依据球直径而定，每一横条带可看成是正截头圆锥管，用放射线法展开，如图3－91所示。具体作法如下：

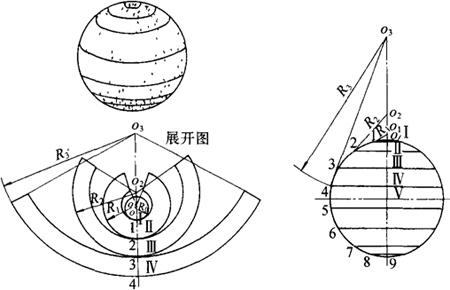
图3－91 球面的分带展开

①用已知尺寸画出球面的主视图，16等分球面圆周，由等分线引水平线(纬线)分球面为两个极帽、七个长条带。其中，中间长条带为圆筒。圆筒展开为一长方形，长边等于球面周长，短边等于等分弧的弦长。其余各长条带为正截头圆锥管，用放射线法展开，展开半径为R₁、R₂、R₃。半径的求法是：连接1－2、2－3、3－4并向上延长交竖直轴线于o₁、o₂、o₃，得R₁、R₂、R₃。

②作展开。极帽展开是以o为圆心R₀(尺₀等于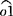弧长)为半径的圆。在过0点的竖直线上取1－2，2－3，3－4等于球面各等分弧的弦长。以2、3、4点为中心取R₁、R₂、R₃向上截取得0₁、0₂、0₃。再以o₁、o₂、o₃为圆心至1、2、3、4点的距离为半径分别画圆弧，取各弧长对应等于球面各纬线为直径的纬圆周长，各扇形带即为所求各长条带的展开图。

从上述可知，作近似展开时，常常以直线代曲线，以平面代曲面，也就是“以直代曲”和“以平代曲”，即以可展的单曲面逼近不可展的双曲面。这是对不可展表面作近似展开时经常应用的方法。

4．球体封头的展开

球体封头的组合形式有许多种，小型的可由整块板料加工成形。大型或大直径的球体封头，由于受原材料尺寸和加工条件所限制，一般采用分块下料拼接制造。如图3－92所示的封头，为高炉用热风炉帽，因为直径较大，由六块板料和极帽拼接制成。展开方法有多种，在此仅介绍其中常用的球面分瓣，既作经线方向的分瓣，又作纬线方向的分带相结合的展开法。此方法是将球面看成由若干纬圆组成，而每一纬圆又在不同锥度的正截头异径圆锥面上(锥底直径)，若求出各圆锥母线(展开半径)，就能展开各纬圆，从而作出球面分瓣的展开图。其具体作法是：

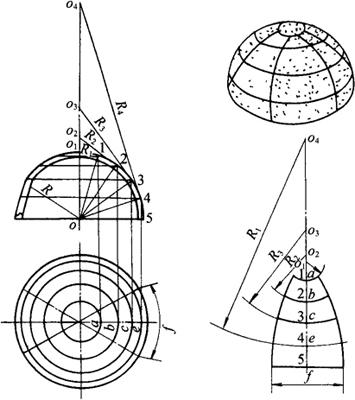
图3－92 球体封头的展开

①用已知板厚中心半径R画出主视图和俯视图。六等分俯视图圆周(图中未注明符号)，过圆心连接各等分点与极帽圆相交，为各块料结合线的水平投影。

②四等分主视图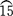，等分点为1、2、3、4、5。过等分点引纬线，并在俯视图中画纬圆，与结合线相交。各纬圆的1／6弧长分别以a、b、c、e、f表示。

③由1、2、3、4点分别引圆的切线交竖直轴延长线于o₁、o₂、o₃、0₄，且以R₁、R₂、R₃、R₄表示各切线长。

④作展开。画竖直线1－5等于主视图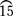弧伸直长度，并照录2、3、4点。以1、2、3、4点为中心取R₁、R₂、R₃、R₄长在5－1延长线上截取得0₁，0₂，0₃，o₄再以各点为圆心，R₁，R₂，R₃，R₄为半径分别画圆弧，取各弧长对应等于俯视图a、b、c、e弧长，再由5点引水平线等于f，得出各点后，分别连成光滑曲线，就是所求半球面的1／6瓣的展开图，如图3－92所示。

极帽展开图是以极帽弧长为直径的圆，图中未画出，可作习题练习。

【例14】 斜螺旋面

斜螺旋面是母线的一端沿着圆柱螺旋线运动，并且母线始终保持与轴线斜交成一定角度而形成的曲面，如图3－93所示。

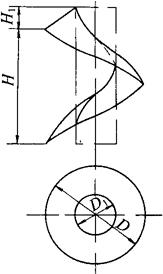
图3－93 斜螺旋面

斜螺旋面投影图作法：作十字中心线，先在两视图中作内螺旋线，作法和上例相同。先把导程H和俯视圆投影圆D₁画出，然后各作12等分，将圆上各等分点1、2、3……向上引铅垂线，过H的12等分点分别作水平线，和铅垂线对应交得1′、2′、3′……各点，光滑连接各点即得斜螺旋面内螺旋线的投影。然后将俯视图中的外圆12等分，根据内外螺旋线差距为H₁，在正视图中作出a′点，1′a′为斜螺旋线的素线长度，和垂直中心线成α角。过a′点起，仍然取导程H长度并作12等分，用和内螺旋线相同的作法，作出外螺旋线，得到的图形即是斜螺旋面的投影图。

斜螺旋面展开图作法：斜螺旋面可用三角形法近似作图。先将俯视图中的ab21四边形分割成a21和a2b两个三角形，以内外螺旋线每等分高度为一条直角边，以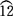和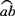弧长为另一直角边作两个直角三角形，求得内外螺旋线每等分的实长l₁和l₂。再以导程差H₁为一直角边，以a2长度为另一直角边作直角三角形，求得斜边长度为l₃，a′1′的长度为a1和b2直线边的实长。

先作线段a1长为实长a′1′，以a为圆心l₃为半径画弧，再以1为圆心l₁为半径画弧交于点2，再以2为圆心a′1′为半径画弧和以a为圆心l₂为半径所画弧交于点b，即得到ab21四边形，依次类推作出所有四边形即得到斜螺旋面在一个导程内的展开图形，如图3－94所示。

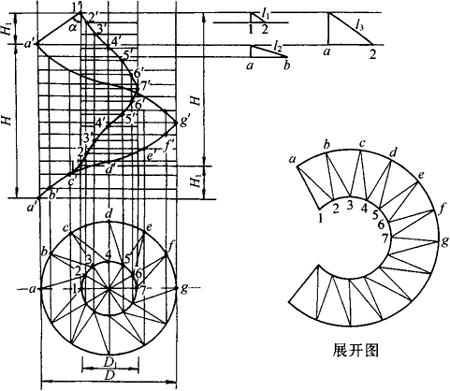
图3—94 斜螺旋面的展开

【例15】 方－方形迂回180°螺旋管

图3－95为方－方形迂回180°螺旋管投影图。

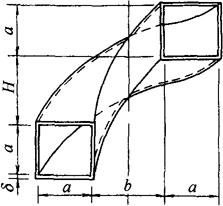
图3－95 方－方形迂回180°螺旋管

此构件由上下面板和内外侧板组成，上下面板是相同的已知半导程的正螺旋面，用内壁尺寸作放样和展开时，素线为a。

上下面板展开图作法：上下面板表面应是素线长度为a，导程为2(h+a)，内导柱直径为b的正螺旋面展开的一半。如图3－96所示，先计算出内外螺旋线长度L和L₁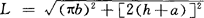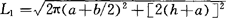，，，则展开内圆半径r=aL／(L₁－L)，R=r+a，缺口外圆弧长l=2πR－L₁，然后以r和R为半径画同心圆，在外圆上截取弧长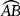等于l，并由A、B两点向圆心引线，交内圆于C、D两点，这缺口ABCD以外的圆环部分对称分开的一半即为上下面板的展开图形，如图3－96(b)所示。

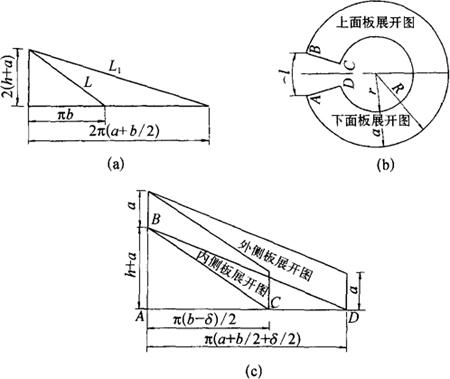
图3－96 螺旋管的展开

内外侧板展开图作法：内外侧板的展开用中径作图。作直角三角形，使一直角边AB长为(h+a)，另一直角边AC长为π(bδ)／2和AD长为π［(a+b)／2+δ／2］，如图3－96(c)所示，在各自三角形斜边上两端作AD边的垂线，长度为a，所得到的两个平行四边形即为内外侧板的展开图形。

【例16】 方－矩形迂回180°螺旋管

图3－97为方－矩形迂回180°螺旋管的投影图。

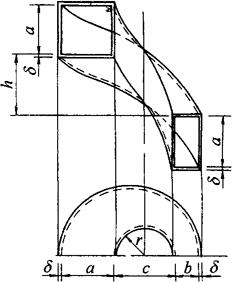
图3－97 方一矩形迂回180°螺旋管

此构件由上下面螺旋面板和内外侧板组成。因矩形口长度和方口等径，上下面板的内螺旋线应是圆柱螺旋线，而外螺旋线是圆锥螺旋线的被圆柱圆锥同时截切的正螺旋面，它的平面投影边线是由圆和圆锥螺旋线组成。

平面放样图的画法：用计算法作图，螺旋线正视图可不画出，仅画中径的俯视图求作展开图。以(cδ)／2和a+(c+δ)／2为半径画半圆环，在半圆环的一边上从内侧取长度(b+δ)的线段，将剩下的a′h′部分作6等分，并将半圆周作同样等分，然后以a′h′上6等分点到圆心O为半径，以O为圆心画弧与圆上各等分线对应交得a′、b′、c′……各点，光滑连接各点得到的螺线和内半圆组成的图形即平面投影放样图形，如图3－98所示。

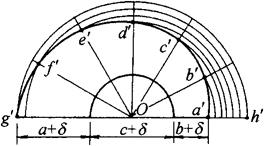
图3－98 螺旋管的平面放样图

上下面板展开图作法：先计算出以a为素线全导程展开的正螺旋面的一半，再按图3－98的作法减去素线由a到b多余的部分即可得到上下面板的展开。先作全导程计算如图3－99(a)所示，内螺旋线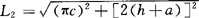，外螺旋线长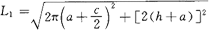，然后用L₁和L₂的值计算出展开内圆半径和外圆半径r，R，计算式为r=aL₂／L₁－L₂、R=r+a、展开缺口外弧长l=2πR－L₁，然后如图3－99(b)所示作出正螺旋面的扇形展开图ABCD，在素线AB边上截取AE等于矩形宽度b，将余下BE部分6等分并将外圆周螺纹线同样作6等分，以O为圆心以各等分点到O距离为半径画弧，和各等分连线对应交得E、2、3……各点，光滑连接各点得螺线，螺线和内半圆组成的图形即是上下面板的展开图形。

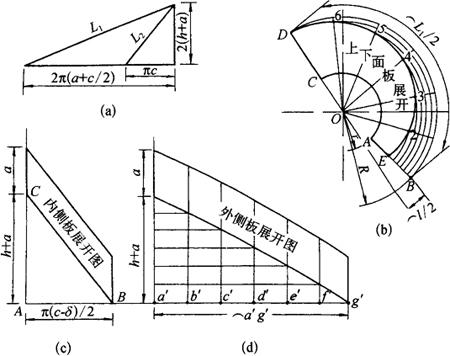
图3－99 螺旋管的展开

内外侧板的展开图作法：侧板煨圆用中径展开。作直角三角形，使一直角边AC等于(h+a)，另一直角边AB长度为π(c－δ)／2，斜边就是内侧板边线长度。分别过B、C两点作垂直于AB的线段，且线段长度为a，得到的平行四边形即是内侧板的展开图，如图3－99(c)所示。外侧板展开方法相同，使三角形一直角边为(h+a)，另一直角边长为图3－98中外螺线弧长，并同样截取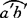、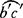……各弧长度，并将(h+a)边也作6等分，过各等分点作水平线和a′、b′……各点向上引的垂线对应交于各点并光滑连接各点，过曲线上各点向上移动距离a，得各点并光滑连接即得外侧板展开，如图3－99(d)所示。