橘瓣球壳瓣片料计算

出处：按学科分类—工业技术 江苏科学技术出版社《铆工实用技术手册》第244页（5897字）

图3－123 立体图

球形贮罐按分瓣方式分为橘瓣式、足球瓣式、混合瓣式等几种，常用的为橘瓣式，如图3－124所示。其特点是球壳拼装焊缝较规则，施工简便，加快组焊进度，便于采用自动焊。由于分块分带对称，装配应力及焊接内应力较均匀。下面介绍其计算方法。

图3－124 1000m³橘瓣球体

计算原理见图3－125。

图3－125 计算原理图

1．赤道带

(1)展开料计算方法(见图3－125和图3－126)

图3－126 赤道带展开图

①半纵向长(mm)

②纵向每等份弧长(mm)

③每等份所对球心角

④每等份点处截圆半径R_n=R·cosnQ′₁

R₂=6150×cos5°=6126．6(mm)

同理得：

R₁=6150mm，R₃=6056．6mm，R₄=5940．4mm

R₅=5779．1mm，R₆=5573．8mm，R₇=5320．1mm。

⑤各等份点横向弧长(赤道带分12瓣片，每片球心角为30°)

同理得：

S₁=3220mm，S₃=3171．2mm，S₄=3110．4mm，

S₅=3025．9mm，S₆=2918．4mm，S₇=2788．7mm。

⑥上口展开半径P₇=R·tan(Q₂+Q₃)=6150×tan60°=10652．1(mm)

(2)成形后尺寸计算方法(见图3－127)

图3－127 赤道带成形后尺寸

1)端口尺寸

①上口截圆半径R′=R·cosQ₁=6150×cos30°=5326．1(mm)

2)纵向尺寸

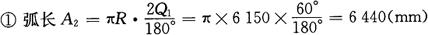
②弦长C₂=2R·sinQ₁=12300×sin30°=6150(mm)

③弦高V₂=R·(1－cosQ₁)=6150×(1－cos30°)=823．9(mm)

3)对角线尺寸

4)中横向尺寸

式中 Q₁——赤道带半球心角；

Q₂、Q₃——分别为温带和极带球心角；

R——球内半径；

m——赤道带瓜瓣数，本例m=12

2．温带

(1)展开料计算方法(见图3－127和图3－128)

图3－128 温带展开图

④每等份点处截圆半径R_n=R·cos(Q′₁+nQ′₂)

R₇=6150×cos30°=5326．1(mm)

R₈=6150×cos35°=5037．8(mm)

同理得：

R₉=4711．2mm，R₁₀=4348．7mm，R₁₁=3953mm，R₁₂=3527．5mm，R₁₃=3075mm。

⑤各等份点横向弧长(温带分12等份，每等份30°)

同理得：

S₈=2637．8mm，S₉=2466．8mm，S₁₀=2277mm，

S₁₁=2069．8mm，S₁₂=1847mm，S₁₃=1610mm。

⑥上口展开半径P₁₃=R·tanQ₃=6150×tan30°=3550．7(mm)

(2)成形后尺寸计算方法(见图3－129)

图3－129 温带成形后尺寸

1)上端口尺寸

①截圆半径R″=R·cos(Q₁+Q₂)=6150×cos60°=3075(mm)

2)下端口尺寸

同赤道带端口尺寸。

3)纵向尺寸

4)对角线尺寸

图3－130 对角线弦长计算原理图

②对角线所对球心角(由弦长式推导而得)

3．极板

(1)中央板(见图3－131)

图3－131 极带中央板

1)展开料计算方法

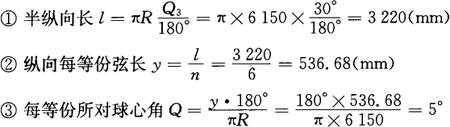
④各等份点处截圆半径R_n=R·cosnQ

R₂=6150×cos5°=6126．6(mm)

同理得：

R₁=6150mm，R₃=6056．6mm，R₄=5940．45mm，

R₅=5779mm，R₆=5573．8mm，R₅=5326mm。

同理得：

S₁=2790．8mm，S₃=2748．4mm，S₄=2695．7mm，

S₅=2622．5mm，S₆=2529．3mm，S₇=2416．9mm。

⑥端口展开半径P₁₃=R·tanQ₃=6150×tan30°=3550．7(mm)

2)极带中央板成形后尺寸计算方法(见图3－132)

图3－132 极板中央板成形后尺寸

①端口尺寸：

A．极板截圆半径R′=R·sinQ₃=6150×sin30°=3075(mm)

②两侧角部间纵向尺寸

C．弦高V=R·(1－cosα)=6150×(1－cos27．28°)=683．9(mm)

③中横向尺寸：

B．弦长C=2R·sinQ₃″=2×6150×sin13°=2766．9(mm)

C．弦高V=R·(1－cosQ₃″)=6150×(1－cos13°)=157．6(mn)

④对角线(纵中线)尺寸：

B．弦长C=2R·sinQ₃=12300×sin30°=6150(mm)

C．弦高V=R·(1－cosQ₃)=6150×(1－cos30°)=823．9(mm)

(2)边板(见图3－133)

图3－133 极带边板

1)边板左部分

④每等份点所处截圆半径R_n=R·cosQ_n

R₂=6150×cos4．5461°

=6130．65(mm)

同理得：

R₁=6150mm，R₃=6072．73mm，R₄=5976．6mm，R₅=5842．85mm，R₆=5672．35mm，R₇=5466．15mm。

同理得：

S₁=912．4mm，S₃=900．9mm，S₄=886．6mm，

S₅=866．8mm，S₆=841．5mm，S₇=811mm。

2)边板右部分

②每等份弧长y(同边板左部分的计算)。

③每等份所对球心角Q(同边板左部分的计算)。

④各等份点所处纬圆半径R_n(同边板左部分的计算)。

⑤各横向弧在其截圆上的圆心角λ_n(左部分皆为8．5°，而右部分各异)。

式中 Q——中线一等份所对球心角，从边板左部分已知为4．5461°；为定值。

同理得：

λ₃=7．212°，λ₄=5．482°，λ₅=2．779°，

λ₆=－1．376°，λ₇=－8．5°

⑥各等份点横向弧长(R_n同边板左部分的R_n)

同理得：

S₂=875．8mm，S₃=764．4mm，S₄=571．8mm，

S₅=283．4mm，S₆=136．3mm，S₇=811mm。

3)极板边板成形后尺寸(见图3－134)

图3－134 极板边板成形后尺寸

①左部分纵向尺寸

C．弦高V₁=R·(1－cosβ)=6150×(1－cos27．276°)=683．9(mm)

②右部分纵向尺寸

C．弦高V₂=R·(1－cosβ)=6150×(1－cos21．44°)=425．6(mm)

③横中线尺寸

④右部分大小弧长

A．极板的截圆半径R″=R·sinQ₃=6150×sin30°=3075(mm)