质量管理中的定量分析

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第594页（6113字）

在质量管理中，如果没有定量分析，就没有明确的质量概念，就不能找出科学的规律，并进行科学的管理。因此，进行统计的质量管理，必须收集数据，研究数据。收集数据的目的不外乎以下几点：(1)掌握生产现状；(2)分析质量问题的原因；(3)控制生产过程；(4)调整工序；(5)判断产品质量是否符合标准等。

1．在运用和收集数据时要注意的问题

(1)用正确的数据说话。要根据事实作出判断和采取行动。数据应是正确的记录，要考虑现场情况来设计记录的方式方法。来历不明的、虚假的数据不但无用，而且有害。

(2)数据必须加工。原始数据往往是多方面的，只有经过适当加工，才能把本质揭露出来，才能正确反映客观事实。加工步骤随目的的不同而异。通常可按收集的目的进行分类、画图、计算而整理出来。

(3)数据必须进行分析。将经过加工的数据，结合工艺理论、现场观察、实验验证以及日常经验进行分析，掌握现实情况，找出问题，提出保证或改进产品质量的措施，并进一步检查这些措施是否有效，是否得到贯彻。

2．数据的分类

根据测定的对象和数据的来源不同，数据可分为计量值数据和计数值数据两类。

(1)计量值数据。凡是可以连续取值的，或者说可以用测量工具具体测出小数点以下数值的这类数值叫做计量值数据。如长度、容积、重量、化学成分、温度等等。就长度来说。在1－2毫米之间，还可以连续测出1．1，1．2，1．3毫米等等数值来。

(2)计数值数据。凡是不能连续取值的，或者说即使用测量工具也得不到小数点以下的数据，而只能得到0或1、2、3、4……等自然数的这类数据，叫做计数值数据。如废品件数、不合格品件数、疵点数、缺陷数，等等。如废品件数，就是用卡板、塞规去测量，也只能得到1件、2件、3件……等等废品数。计数值数据还可以细分为计件值数据和计点值数据。计件值数据是指按件计数的数据，如不合格品件数、不合格品率等；计点值数据是按点计数的数据，如疵点数、焊缝缺陷数、单位缺陷数等。

在质量管理中，并不是所有质量都有一些现成的数据可以收集和直接来加以统计的。有时需要人为地定出一些数字来进行统计。如评定分数就是一个常用的方法，人为地评上3分、5分、10分等，或者一等品、二等品、三等品等等。

3．数据的收集方法

搜集数据往往都是对其中某个对象，随机地抽取若干个作为代表进行调查，此时被调查的全体称为总体，而抽出来的调查对象称为样本，样本中的每个产品称为样品。表达样本性质的叫做统计量，表达总体性质的叫做总体量。统计方法的任务就是通过统计量对总体量进行推测。总体可以分为有限总体和无限总体两类。在生产中以了解产品(或半成品)的整批情况为目的的整体称为有限总体；在进行的工序控制时，是把按照某一工艺标准进行的工序当作总体，这时的总体叫做无限总体。

为了使被抽取的数据能尽可能正确地代表整批数据的情况，就需要随机地抽取数据。所谓随机抽取，就是整批数据中的每一个数据都有同等的机会被抽到。随机抽样有很多种方式，常用的有以下几种。

(1)单纯随机抽样

这就是通常所说的随机抽样法。这种随机抽样可以用抽签的办法，也可以用查随机数值表的办法，还可以用掷随机数骰子的办法等等。例如，要从100件产品中，随机抽取10件组成样本。我们可以把这100件产品从1开始编号一直编到100号，然后用抽签的办法，任意抽取10张，假如正好抽到的编号是3，7，15，19，23，35，46，51，77，89等10个，于是就把这10个编号的产品拿出来组成样本。这就是单纯随机抽样。这个办法的优点是抽样误差较小，缺点是抽样手续比较繁杂。

(2)分层随机抽样

这就是事先把在不同生产条件(如人、机、料、方法、环境等)制造出来的产品归类分组，然后再按一定的比例从各组中随机抽取产品组成样本。例如有甲、乙、丙3个工人在同一台机器设备上，倒班干同一种零件(他们加工完了的零件，分别放在三个地方)，如果现在要求抽取15个零件组成样本．其办法是，从堆放零件的三个地方，每个地方随机抽取5个零件，合起来一共15个零件组成样本，这就是分层随机抽样。这种抽样方法的优点是样本的代表性比较好，抽样误差小，缺点是抽样手续比较单纯。这种方法常用于产品质量验收。

(3)整群随机抽样

这种抽样方法的特点，不是一次随机抽取一个产品，而是一次随机抽取若干个产品组成样本。例如，对某种产品来说，每隔一定时间(例如30分钟、1小时、4小时、8小时等)一次抽取若干个(几个，十几个，几十个等)产品组成样品。这种抽样方法的优点是抽样手续简便，缺点是样本的代表性差，抽样误差大。这种方法通常用在工序控制中。

4．质量特征数

总体的质量分布一般可以根据样本数据的统计性质进行推断。在质量管理中常用的统计特征数可分为两类：一类是表示数据的集中位置的，如样本平均数、中位数等；一类是表示数据的分散程度的，如极差、样本方差、样本标准偏差等。

(1)平均数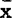

平均数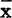是表示算术平均值，它是表示质量数据集中位置的各种特征数中最基本的一种，其计算公式如下：

式中：n——样本大小；

∑——求和符号；

x_i——任意一个数据(i=1，2，3，…，n)

(2)中位数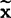

中位数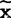也是表示数据集中位置的一种特征数。如果把收集到的质量数据x₁，x₂……，x_n，按大小顺序重新排列，则排在正中间的那个数就叫做中位数，用符号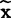表示。例如1、3、4、2、5这五个数据的中位数x=3。如果数据个数n为偶数，正中位置有两个数，此时，中位数为正中两个数据的算术平均值。例如，1、2、3、5、4、6，则其中位数为：

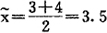
用中位数来表示数据集中位置比用样本算术平均数来表示要粗略一些，但是可以减少计算的工作量。

(3)样本方差S²

样本方差是表示质量数据分散程度的特征数，其计算公式如下：

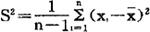
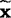式中：S²——样本方差；——某个数据与样本平均值之间的离差。

(4)样本标准偏差S

标准偏差也是表示质量数据分散程度的特征数，并且是最重要的质量特征数。

根据国际标准化组织规定，把样本方差的正平方根作为样本标准偏差，符号S表示如下；

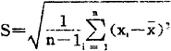
(5)极差R

极差是指数据中最大值与最小值之差，一般用符号R表示。例如，有五个数：40、50、60、60、90，则极差R=90－40=50。

极差是表示数据分散程度的各种特征数中最简单的一种。但是由于只用了最大与最小的数据没有充分利用数据提供的信息，因此反映实际情况的精度较差。

5．质量控制中的概率分布

从单个产品来说，由偶然原因引起的差异是随机的，其数值可正可负、可大可小，但从整批产品来观察，偶然原因引起的产品质量差异却有一定的规律性。如果将产品质量特性(尺寸、重量、抗拉强度等)分成若干组、计算每组的产品数并画出图表，即以产品质量特性作为横坐标，产品的数量作为纵坐标，以各个矩形的高度表示各组的产品数，画成一个质量分布图(如图5．4．5－1所示)。如果这批产品的数目愈来愈多，分组愈来愈细，即组数分得相当多，图形就会转化为一条光滑的曲线，这条曲线就称为质量分布曲线。

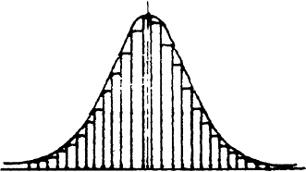
图5．4．5－1

数理统计可以证明，在正常情况下，以重量、尺寸、直径、强度等表示的产品质量特性，其分布曲线都是这样的形状。这条曲线称为正态分布曲线，它的数学方程式是：

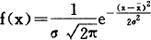
式中：f——正态分布曲线的纵坐标值，即各种尺寸或重量的产品数；

x——正态分布曲线的横坐标值，却尺寸或重量等各种质量特性的数值；

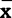——各种尺寸、重量数据的算术平均数；

σ——各种尺寸、重量数值的标准偏差；

л——圆周率(л=3．1416)；

e——自然对数的底(e=2．7183)。

正态分布曲线具有以下几个性质：

(1)分布曲线对称于直线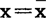，即以算术平均数为中心，左右对称。

(2)当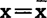时，曲线处于最高点，当x向左、右远离时，曲线不断地降低，整个曲线呈现中间高、两边低的形状。

(3)如果曲线与横坐标轴所围成的面积等于1，则：

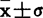范围内的面积占68．26%；

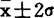范围内的面积占95．45%；

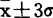范围内的面积占99．73%。

质量特性在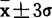范围以外的产品是非常少的，不到千分之三。

根据正态分布曲线的这种性质，可以认为：凡是在范围以内的质量差异都是正常的，不可避免的，是偶然性因素作用的结果；如果质量差异超过了这个界限，则是系统性因素造成的，说明生产过程中发生了异常现象，需要立即查明原因进行改正。在生产进行过程中，就可以根据这个理论控制产品的质量。

在质量控制中，常用的分布除了正态分布外，还有超几何分布、二项分布、泊松分布等等。

6．工序能力和工序能力指数

为了进行质量管理，必须了解生产过程的工序能力。工序能力是指该生产过程能满足质量要求的能力，即在稳定状态下，生产过程生产合格品的能力。这里强调的是质量方面的能力，不能与一般所说的生产能力混为一谈。工序能力是原材料、设备、操作方法、操作人员、检测方法和环境等质量因素共同作用的综合结果。只有在工序呈现稳定状态时表现出来的能力。才能真实地反映出该工序的实际能力。工序能力用6倍的产品标准偏差(即6σ)表示。

为了准确地估计工序能力满足产品质量要求的程度，引入了工序能力指数这个概念。所谓工序能力指数，就是图纸或标准要求的公差范围与工序能力的比值。工序能力指数的计算如表5．4．5－1所示。

表5．4．5－1 工序能力指数C_p，C_pk计算式表

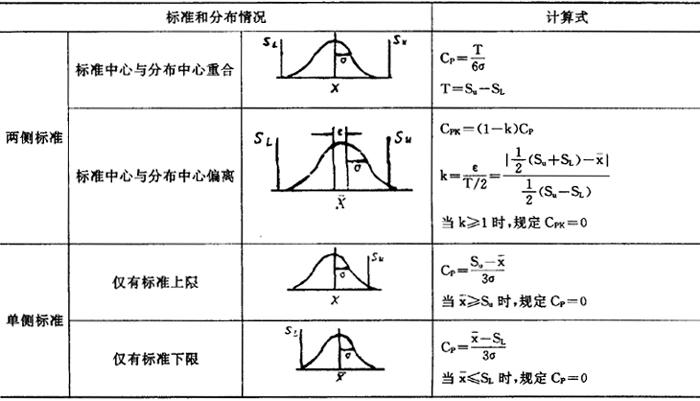
表中：T－公差；S_u－公差上限；S_L－公差下限；ε－偏移量；k－偏移系数；σ－标准偏差(由样本标准偏差S来估计)

工序能力指数判断标准如表5．4．5－2所示。

表5．4．5－2 工序能力指数判断标准

工序能力调查一般按下列步骤进行。

(1)明确调查的目的。调查的目的是为了摸清某道工序保证产品质量的能力大小；

(2)选择调查对象。根据调查目的来选取被调查的工序和项目；

(3)确定调查方法。包括决定调查范围、分层方法、调查期限、抽样方法、样本大小等内容：

(4)工序的标准化。即对被调查工序的操作者、机器设备、使用的废材料、操作测量方法和工作地布置等制订出各项标准；

(5)严格按照各项标准进行作业；

(6)搜集数据；

(7)画直方图或分析用控制图或工序能力图等；

(8)判断工序是否处于控制状态；

(9)计算工序能力指数；

(10)处理。即采取各种措施提高工序能力，进行PDCA循环，并将工作成果、正反面的经验纳入标准，实行标准化。