幂级数的运算性质

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第219页（539字）

幂级数的四则运算 设有两个幂级数和的收敛半径分别为R₁和R₂，则

其中

其收敛半径R视具体的两个幂级数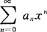和而定，可能R比R₁和R₂要小得多．

幂级数的分析运算

(1)幂级数的和函数S(x)在开区间(－R，R)内(R为收敛半径)连续．

(2)设幂级数在收敛区间(－R，R)(R为收敛半径)内收敛于S(x)，则幂级数可以逐项积分，即

此性质称为逐项积分法．

(3)设幂级数的和函数S(x)在收敛区间(－R，R)(R为收敛半径)内可导，其导数可从幂级数逐项求导得到，即

其收敛半径仍为R．此性质称为逐项微分法．

(4)性质(3)可以连续使用，即