回转面构件

出处：按学科分类—工业技术 江苏科学技术出版社《铆工实用技术手册》第225页（2326字）

曲线旋转面和螺旋面一样属于不可展曲面，这类形体的构件如储罐罐顶、球罐等都属于较大型结构，一般要多块钢板拼接起来，在制造中往往是先下毛坯料成形后再二次下料。关于二次下料的毛坯料展开请参见相关章节，本段只介绍用等曲线法的近似展开方法和可以一次直接下料的构件。这类构件在制造中由于冷热加工方法的不同，成形后边缘尺寸和展开尺寸有很大差距，所以往往要在展开时用经验近似展开或修正。

【例17】 拱顶罐分瓣搭接顶板

图3－100为拱顶罐顶盖的施工图。

图3－100 拱顶罐顶盖施工图

因图纸要求顶盖每块顶板之间是搭接，所以可以直接近似展开下料，以中径作图和展开。顶板可用放样法作图，一般在罐底有较大面积可直接作图展开，在没有条件的情况下可用计算法展开。

放样展开图作法：如图3－101所示，作出一块顶板的正视图和俯视图，俯视图中不包括40mm的搭接部分。将正视图中分瓣搭接顶板圆弧作若干等分，过各等分点作圆的切线交轴线于各点得R₁、R₂、R₃等各半径线。将这些等分点投影到俯视图中得B′、C′、D′点。再以O′为圆心以B′、C′、D′点到O′点距离为半径画弧，得到一块顶板间的弧长l₁、l₂、l₃。然后在展开图中取线段bd等于正视图中长度，取线段，过b、c、d各点用对应R₁、R₂、R₃为半径画弧，在弧上以对应俯视图中的l₁、l₂、l₃值取弧长得到一系列点，光滑连接各点就得一块顶板边线的展开曲线，然后在曲线上一边加上40mm的搭接部分就得到顶板的全部展开图形。

图3－101 罐顶板样展开图

计算法展开作图：计算法作图需要计算出展开图中R_n、L_n和l_n值就可以直接作展开图形。

计算公式： R_n=r tanΦ_n

l_n=0．017453αr sinΦ_n

L_n=0．017453r(Φ_n－β)

式中 r——球放样半径；

α——每块球瓣在平面投影中所含圆心角；

β——球瓣径向到球轴线最小圆心角；

Φ_n——球瓣任意位置径向对应圆心角；

l_n——对应Φ_n任意位置纬向弧长；

L_n—－对应Φ_n值的展开用半径。

本例中已知r等于4203mm，顶板分12块即每块的对应夹角α=30°、β=arcsin(700mm／4203mm)=9．58716°，而顶板Φ_n的最大值在图3－101中可看出应是Φ₂=arcsin(2105mm／4203mm)=30．0551°，将以上已知数值代入以上三公式中，Φ_n以同样等分分别计算，所得数值见表3－15。

表3－15 罐顶盖板展开计算值

计算法展开作图：因是程编计算十分方便，所以Φ_n可以取较多的值进行计算，如形状要求不太严时可减少计算点。此计算法展开经长期实践证明是较准确的计算展开，因此搭接顶盖可用此法直接计算展开，作图法和放样作图法相同，如图3－102所示。

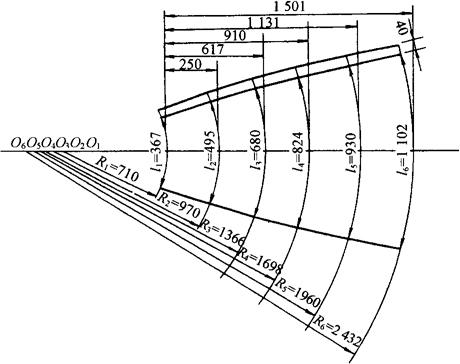
图3－102 罐顶板计算展开图

【例18】 分瓣球带

图3－103为分瓣球带的示意图。

图3－103 球带分瓣图

本例半球瓣中球缺部分的展开可参见其他例，本例仅作温带球瓣的展开。如果用例16的方法展开则半径过大而无法作图，所以一般用球的正视图中弧长为半径来作图。实践证明这样作出的图形需要作适当的修改进行补料处理以保证展开尺寸尽量逼近实形。本例不考虑板厚处理用中径放样和展开。

分带球瓣的展开作图方法如图3－104所示，在正视图中将球瓣中心弧长分成若干等份，过各等分点向下作OA的垂线交俯视图水平轴线于a、1′、2′、…、b各点，以O₁为圆心以a、1′、2、…、b各点到O₁的距离为半径画弧，在这块球瓣的俯视图的投影的两边线内得到一系列弧长。在OA的延长线上取线段O′A′等于正视图中弧长，并取B′点使A′B′等于，将A′B′作和同样的等分，然后以各等分点到0′点距离为半径以O′为圆心画弧，在各弧上以A′B′为中心线对称取弧段等于俯视图中弧和弧之间的各弧长，得到一系列交点，将这些点光滑连接即得到分割后的近似展开图形，然后在最后一条弧线上将两交点连接，在中线上得D点，将A′D2等分，过等分点作中心线的垂线，和两边轮廓曲线交于D′、D″两点，将D′、D″和A′光滑连接得到补角，此展开图形即为球瓣展开的近似展开图形。此展开方法一般用于赤道带和温带的球瓣展开。

图3－104 球带的分瓣放样展开