构件线段实长求法
出处:按学科分类—工业技术 河南科学技术出版社《钣金技术手册》第393页(3649字)
(一)直线段实长求法
1.旋转法
旋转法求实长,就是将空间一般位置的直线段,绕一垂直于投影面的固定轴旋转成投影面平行线,则该线段在与之平行的投影面上的投影反映实长。如图6-1a所示,以AO为轴将线段AB旋转至与正面平行的AB1位置,线段AB则由任意位置变为正平线位置,其新的正面投影a′b″既为AB的实长。
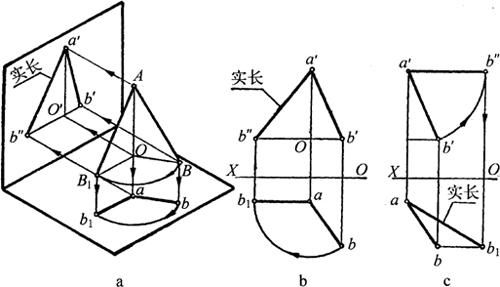
图6-1 旋转法求实线长
a.旋转 b.投影图 c.实长图
图6-1b为AB线段利用旋转法求实长的投影作图,图6-1c则表示将AB线段旋转成水平位置求实长作图过程。旋转法适用于角锥、斜圆锥及其组成构件。
(1)四棱锥棱线实长求法:作四棱锥侧面展开图时须先求出棱线实长,图6-2a中OA棱线为一般位置直线,在主视图、俯视图中均不反映实长。若利用旋转法,以O为圆心、Oa为半径画圆弧至水平中心线,由水平中心线交点引上垂线,交主视图锥底延长线于a″,则O′a″即为棱线OA的所求实长。

图6-2 旋转法求棱线及素线实长
a.四棱锥棱线实长 b.斜圆锥表面素线实长
(2)斜圆锥表面各素线长求法:为了画出斜圆锥表面展开图,须先求出其底圆周各等分点与锥顶连线(简称素线)的实长。由图6-2b可知,这些素线除主视图两边轮廓线(O′-1′、O′-5′)外,均不反映实长。各素线实长可利用旋转法求出。即以O为圆心,O至2、3、4各点距离为半径画同心圆弧,得与水平中心线O-5的各交点,再由交点引上垂线交1′-5′于2′、3′、4′点,连接2′、3′、4′与O′,则得O′-2′、O′-3′和O′-4′即为所求三条素线的实长。
2.三角形法
三角形法求直线实长,既可作在主视图中,也可作在俯视图中。从图6-1中可以看出,AB线经过旋转所求出的实线长a′b″,也可以利用三角形法求出其实长,即在图6-1b中作a′O(作为三角形a′Ob″的一条直角边),而以AB线的水平投影线ab(αb=Ob″)线作直角三角形的另一条直角边,则连接三角形的斜边a′b″即为实长。
三角形法多用于上、下底平行或不平行的构件,至少须画出构件的两面视图。如各种罩类、变径、变向连接管及方圆过渡接头等,应用极广。
(1)圆方过渡接头的实长线求法:如图6-3和表6-1所示。
表6-1 直角三角形作图要领(以图6-3为例)
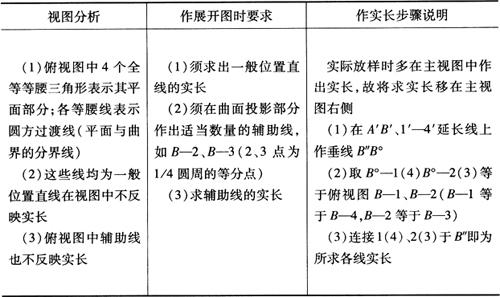
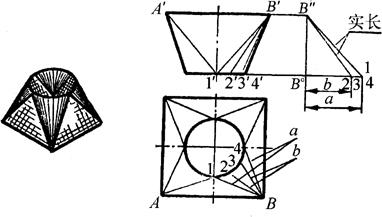
图6-3 直角三角形法求实长
a.圆方过渡接头立体图 b.实长图
(2)顶口倾斜圆方过渡接头的实长线求法:图6-4所示的顶口倾斜圆方过渡接头的表面是由平、曲混合面组成。平面与曲面的过渡线及作展开图时所作的辅助线,均不反映实长。通常采用三角形直角梯形法求其实长,如图6-4a所示,其作图原理是利用另加一辅助投影面,使其轴线平行于求线的原水平投影,且二者对应高度相等,对应高端点的连线反映求线的实长。求解步骤如下:

图6-4 三角形直角梯形法求实长
a.作图原理 b.主视图 c.立体图和顶底断面图 d.实长图
1)用已知尺寸先画出斜圆方过渡接头的主视图和顶底断面图(图6-4b、c)。
2)四等分顶断面半圆周,由等分点2、3、4向1-5分别引垂线,得垂足2′、3′、4′,分别连接2′、3′与A′和3′、4′与B′(图6-4c)。
3)用直角梯形法求实长。图6-4d是为了图面清晰,将主视图左、右轮廓线及作图线分别叠画在同一水平线上求实长图。
由A′(B′)向左截取主视图A′-1、A′-2′、A′-3′得1、2′、3′点,向右截取B′-3′、B′-4′、B′-5得3′、4′、5点。由2′、3′、4′、A′(B′)向上引垂线,取2′-2、3′-3、4′-4等于顶断面2′-2、3′-3、4′-4。再取A′A″(B′B″)等于底断面a/2;连接1、2、3与A″和3、4、5与B″即得所求各线实长。
(3)方漏斗的实长线求法:图6-5a为倒置的方漏斗,顶底断面为正方形互扭45°角,顶口与水平成任意角度倾斜,各棱线长在图6-5两视图中均不反映实长,可采用三角形支线法求其实长,即以求线的某一投影长度作底边,以另一视图中的直高作对边,所成的直角三角形的斜边反映求线的实长。求解步骤如下:
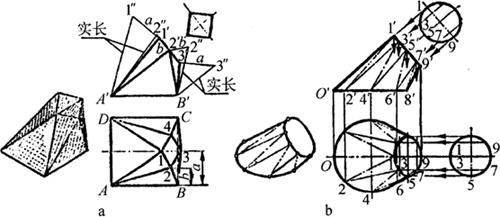
图6-5 三角形支线法求实长
a.方漏斗的实长线 b.斜马蹄的实长线
1)用已知尺寸画出方漏斗的主视图和俯视图。
2)由主视图的1′点作A′-1′的垂线1′-1″等于俯视图中的a长,连接A′-1″即为A′-1′的实长。
3)由主视图的2′点作B′-2′的垂线2′-2″等于俯视图中的b长,连接B′-2″即为B′-2′的实长。
4)同理可求出A′-2′、B′-3′的实长A′-2″、B′-3″。
图6-5b为斜马蹄的立体图及用三角形同心断面支线法求其实长图,求法步骤同上。
(二)曲线求实长法
1.辅助投影面法
辅助投影面法是另增设一个与曲线平面平行的辅助投影面,则曲线在该面上的投影反映实长(图6-6a),这种方法简称为换面法,仅适用于平面曲线。
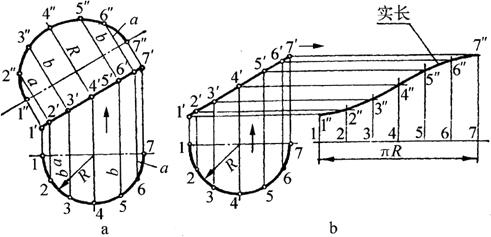
图6-6 平面曲线实长作图求法
a.换面法求法 b.展开法求法
由图6-6a的两视图中可以看出,曲线位于正垂面上,由于正垂面垂直于正投影面、倾斜于水平面,因此曲线的正投影积聚成直线,水平投影为半圆,不反映实形或实长,可加一辅助投影面反映其实长。求解步骤如下:
(1)用已知尺寸画出主视图和俯视图。
(2)六等分俯视图半圆周,等分点为1、2、3、…、7,由等分点引上垂线得与1′-7′各交点。
(3)画1″-7″平行且等于1′-7′,从1′-7′各点分别向1″-7″引穿越垂线得与1″-7″各交点,并由各交点向上取各线长对应等于俯视图圆周等分点至1-7各线长,得2″、3″、…、6″。
(4)通过各点连线1″-4″-7″曲线即为所求平面曲线的实长。
2.展开法
如图6-6b所示,画水平线1-7等于俯视图半圆周伸直并照由各等分点引上垂线,与由主视图1′-7′各点向右所引的水平线对应交点,得出1″、2″、3″、…、7″各点,连接1″-7″曲线即为所求曲线的实长。
3.计算法
图6-7为一个周节圆柱螺旋线的两面视图,由于它的实长线为直线,求其螺旋线的实长可用作图法(说明从略)和计算法两种,用计算法即用计算公式求其实长,其计算公式为
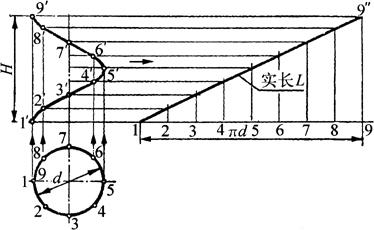
图6-7 计算法求螺旋线实长
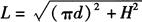
式中 L——螺旋线实长(mm);
d——螺旋线直径(mm);
H——周节长(mm)。