n阶行列式

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第256页（1141字）

n阶行列式的定义 n阶行列式记成

它是取自不同行、不同列的n个元素的乘积

a1j₁a2j₂…anj，₁

的代数和，其中行下标顺排(自然序排列)，列下标j₁，j₂，…，j_n是一个n元排列．当j₁j₂…j_n是偶排列时，该项前面带正号；j₁j₂…j_n是奇排列时，该项前面带负号，即每项的正负号由(－1)^{σ(j1j2…jn)}决定，即

其中表示对所有n元排列求和．由于n元排列共有n!个，故形如

的项共有n!项，(1)式称为n阶行列式的完全展开式．

对角形行列式 行列式

称为对角形行列式．

上三角形行列式 行列式

称为上三角形行列式．

下三角形行列式 行列式

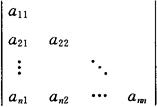
称为下三角形行列式．

对角形行列式、上三角形、下三角形行列式的值等于主对角线上元素的乘积，即

副对角形行列式 行列式

称为副对角形行列式．

左上三角形行列式 行列式

称为左上三角形行列式．

右下三角形行列式 行列式

称为右下三角形行列式．

n阶副对角形行列式、左上三角形、右下三角形行列式的值等于副对角线上元素的积并乘以，即

行列式的等价定义 数的乘法有交换律，对换n阶行列式的完全展式中的任意两个元素，乘积的值不变，但行、列下标均作了一次对换，对换改变排列的奇偶性，但行下标排列和列下标排列的总的奇偶数不变，元素对换若干次，使列下标为顺排(自然序排列)时，则该项的正负号由行下标排列的逆序数决定．