正项级数的审敛法
书籍:数学手册(大学生用)
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第208页(955字)
正项级数的定义 若级数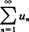 中un≥0(n=1,2,…),则称级数
中un≥0(n=1,2,…),则称级数 为正项级数.
为正项级数.
正项级数收敛的充分必要条件 正项级数 收敛的充分必要条件是:它的部分和数列{Sn}有界,即存在正数M.对任意n,恒有
收敛的充分必要条件是:它的部分和数列{Sn}有界,即存在正数M.对任意n,恒有
|Sn|=|u1+u2+…+un|≤M.
比较审敛法 设 和
和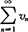 都是正项级数且un≤vn(n=1,2,…).若级数
都是正项级数且un≤vn(n=1,2,…).若级数 收敛,则级数
收敛,则级数 也收敛;若级数
也收敛;若级数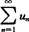 发散,则
发散,则 也发散.用简略的语言叙述即“若大的级数收敛则小的级数也收敛;若小的级数发散则大的级数也发散”.
也发散.用简略的语言叙述即“若大的级数收敛则小的级数也收敛;若小的级数发散则大的级数也发散”.
比较审敛法的极限形式 设 及
及 都是正项级数,如果
都是正项级数,如果
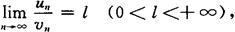
那么级数 和级数
和级数 同时收敛或同时发散.
同时收敛或同时发散.
当l=0时,由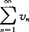 收敛,可知
收敛,可知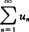 也收敛;
也收敛;
当l=+∞时,由 发散,可知
发散,可知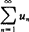 也发散.
也发散.
p-级数 级数 称为p-级数.当p>1时,级数
称为p-级数.当p>1时,级数 收敛;当p≤1时,级数
收敛;当p≤1时,级数 发散.
发散.
设正项级数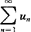 ,如果有p>1,使
,如果有p>1,使 ,则级数
,则级数 收敛;如果有
收敛;如果有 ,则级数
,则级数 发散.
发散.
比值审敛法(或达朗贝尔(D’Alembert)审敛法) 若正项级数 的后项与前项之比值的极限等于ρ,即
的后项与前项之比值的极限等于ρ,即

则当ρ<1时,级数 收敛;当ρ>1时,级数
收敛;当ρ>1时,级数 发散;当ρ=1时,级数
发散;当ρ=1时,级数 可能收敛也可能发散.
可能收敛也可能发散.
积分审敛法(柯西积分准则) 设 为正项级数,若连续函数f(x)在区间[1,+∞)上单调递减,且un=f(n)(n=1,2,…),则级数
为正项级数,若连续函数f(x)在区间[1,+∞)上单调递减,且un=f(n)(n=1,2,…),则级数 与广义积分
与广义积分 有相同的收敛性.
有相同的收敛性.
拉阿伯审敛法 设 为正项级数,如果
为正项级数,如果

则当R>1时,级数 收敛;当R<1时,级数
收敛;当R<1时,级数 发散;当R=1时,级数
发散;当R=1时,级数 可能收敛也可能发散.
可能收敛也可能发散.
上一篇:斯托克斯公式 环流量与旋度
下一篇:数学手册(大学生用)目录