初等变换与初等矩阵
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第282页(2408字)
初等变换 下面三种变换
(1)以非零常数k乘矩阵的某一行;
(2)将矩阵的某两行对换位置;
(3)将矩阵的某一行乘以常数c并加到另一行.称为矩阵的初等行变换.分别称为(1)倍乘变换;(2)对换变换;(3)倍加变换.
同样也可对矩阵的列做上述三种变换,称为矩阵的初等列变换.
矩阵的初等行、列变换统称为初等变换.
初等矩阵 将单位矩阵做一次初等变换得到的矩阵称为初等矩阵.
(1)单位矩阵的第i行(第i列)乘k倍得到的初等矩阵记作Ei(k),称为初等倍乘矩阵,即
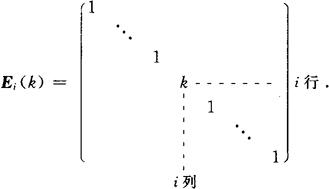
(2)单位矩阵的第i行和第j行(也是i列与j列)互换得到的矩阵记为Eij,称为对换初等矩阵,即
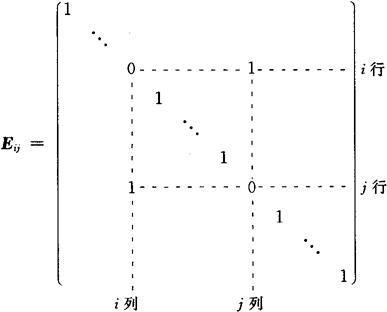
(3)单位矩阵的第i行的c倍加到第j行(也是第j列的c倍加到第i列)得到的矩阵记为Eij(c),称为倍加初等矩阵,即
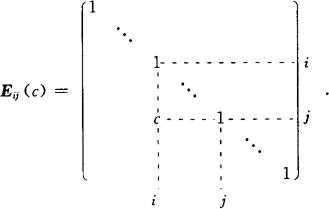
初等矩阵都是可逆矩阵,且
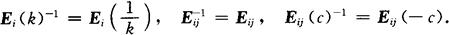
初等矩阵的作用
(1)矩阵Am×n的左边乘一个m阶初等矩阵相当于对A施行一次相应的初等行变换.
(2)矩阵Am×n的右边乘一个n阶的初等矩阵相当于对A施行一次相应的初等列变换.
(3)可逆矩阵经过若干次初等行变换后必可化为单位矩阵,即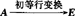 .
.
(4)n阶矩阵A可逆的充分必要条件是A可表示成一系列初等矩阵的乘积,即
A=P1P2…PN 其中Pi(i=1,2,…,N)是初等矩阵.
(5)A是m×n阶非零阵(假设第1列非零),则经过有限次的初等行变换化成如下的阶梯形矩阵:
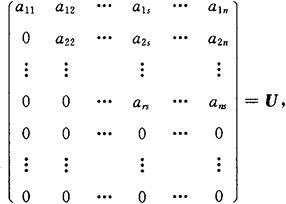
即存在初等矩阵P1,P2,…,PN.使得
PN…P2P1A=U.
r阶子式 设A是m×n矩阵,在A中任取r行,任取r列,它们的交点元素按原来的位置次序组成的r阶行列式称为A的一个r阶子式.
矩阵的秩 矩阵A的不等于零的子式的最高阶数称为A的秩,记作r(A).
初等变换与秩的关系
(1)初等变换不改变行列式的非零性.
(2)初等变换不改变矩阵的秩,即r(Am×n)=r(P1A)=r(AQ1)=r(P1AQ1)=r(PA)=r(AQ)=r(PAQ),其中P1为m阶初等矩阵,Q1为n阶初等矩阵,P是m阶可逆矩阵,Q是n阶可逆矩阵.
阶梯形矩阵的秩 阶梯形矩阵的秩等于阶梯的个数.
求秩的方法
(1)用定义
由小到大,逐个检查各阶子式是否为0,若A的全体元素为零,则r(A)=0.若有非零元素,则r(A)≥1.检查全体二阶子式,若存在一个二阶子式不等于0,则r(A)≥2.若全体二阶子式全为0,则r(A)=1,….若存在一个r阶子式不等于零,所有r+1子式全为零,则r(A)=r.
(2)用初等变换
利用初等变换(行、列变换均可,行、列混合变换也行)化成阶梯形矩阵,阶梯形矩阵中台阶的个数即是矩阵的秩.
等价矩阵 若矩阵A经过初等变换化成为B(即若存在可逆矩阵P,Q,使得PAQ=B),则称A等价于B(或A相抵于B),记作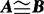 .
.
矩阵等价的性质
(1)反身性: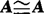 .
.
(2)对称性:若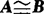 ,则
,则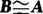 .
.
(3)传递性:若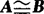 ,
,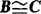 ,则
,则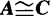 .
.
等价标准形
若A是m×n矩阵,r(A)=r,则
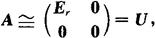
其中Er为r阶单位矩阵,即存在m阶可逆矩阵P,n阶可逆矩阵Q,使得
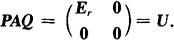
右端矩阵U称为A的等价标准形(与A等价的最简矩阵).
矩阵等价的充要条件
同型矩阵A,B等价,即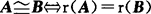 .
.